20  LI-6800 JIP test 分析

暂无时间修改，请参考：

jiptest 简明教程

20.1 参考视频

习惯看视频的也可以参考：

jiptest 演示视频

20.2 关于 Area 和 Sm 参数计算的说明

具体参数的计算参考了 Tsimilli-Michael (2019) 和 Bussotti 等 (2010)，时间轴的单位是 ms。

在最初的版本中，面积计算原本是用了了一个 三次项样条插值来将数据点拟合为一条曲线，然后对曲线进行计算，前几天有客户询问我计算报错，我只能看出来那是积分错误，但我不知道原因，因为积分的方法我是用的一个叫做 MASS 包来处理的，它有一些问题需要处理：

  1. MASS 有时候改动会导致计算面积不能使用，这个发生过一次，好在改动不是特别大，我修改了之后就能用了。但这就是个问题，依赖别人的软件包，作者我也不认识，人家更新不会通知我，也不会管我能不能用。

  2. 样条插值尽管拟合效果不错，但总会因为 J 点和 I 点的拐点导致拟合不佳的情况出现，这样子会带来一定的误差来源。

  3. 基本出错我很难定位具体原因。

基于上面这些原因，我使用了下面的方式对面积计算进行修改，当然下面演示的是原理部分，所以我只计算曲线下部面积，反正上部面积是总面积减去下部面积，所以这个不影响最终计算，也能简化我对计算方式的描述。

20.2.1 曲线下部面积的计算

计算方法依据这里 Sotos 的回答来进行。

基本思路是这样，既然一种积分的方式是将曲线划分为很多个梯形，然后求其总面积。因为我的数据点数量非常大（通常 250 kHz 的调制频率），那么实际上我已经在 1 s 的测量时间内，将曲线划分为 250 kHz - 1 个梯形了（理论上最大值，实际没这么多），那我干脆不用拟合来做曲线，就直接用线连接所有数据点，不久避免了拟合不准确的问题了吗？为简化流程，我将梯形看做矩形，长度使用 2 点滚动平均值来计算，减少误差。因此，下面的内容就是用连续光信号来验证这个观点。

Code
# 使用的软件包
library(zoo)
# 导入依次 OJIP 测量整理好的数据
ac <- read.csv("data/dctest.csv")

# 将数据里的 s 转化为 ms
ac$SECS <- (ac$SECS)*1000

# 使用对数的时间轴
ac$logs <- log(ac$SECS)

# 找到 FO点，因为计算是 OJIP 时间段内的数据
j <- which(ac$FLUOR == max(ac$FLUOR))
# 只选择需要的数据
ac <- ac[1:j,]
# 数据的行数
n <- nrow(ac)

# 使用上面叙述的原理来计算总面积
auc <- with(ac, sum(diff(logs)*rollmean(FLUOR,2)))
auc
[1] 2543274
Code
# 滚动平均值使用的数据，也就是矩形的长
roll <- with(ac, rollmean(FLUOR,2))

# 按照相邻两点多最大值计算最大的误差
auc_max_rect <- with(ac, sum(diff(logs)* FLUOR[2:n]))

# 计算的 sm 参数的最大误差
sm_error <- (auc_max_rect - auc)/(max(ac$FLUOR) - min(ac$FLUOR))

这里 Area 误差从数值上看上去不小，但这是没有标准化后的荧光信号强度，实际并不大，而且没有标准化的数据在荧光参数里多数没有比较的价值，我们看一下标准化后的 Sm 参数：

Code
sm_error
[1] 0.01855341

这个数值是 0.0185534，也就是最大的误差是这个数据，但实际上我们按照梯形最高的边来作为矩形的长来计算的最大面积，这个面积对数据高估了，实际上的误差应该略大于 sm_error/2，也就是 0.0092767，相比于我们的实验来讲，这个小数点后第三位的误差可以忽略不计。

通过图形我们可以直观的观察一下结果：

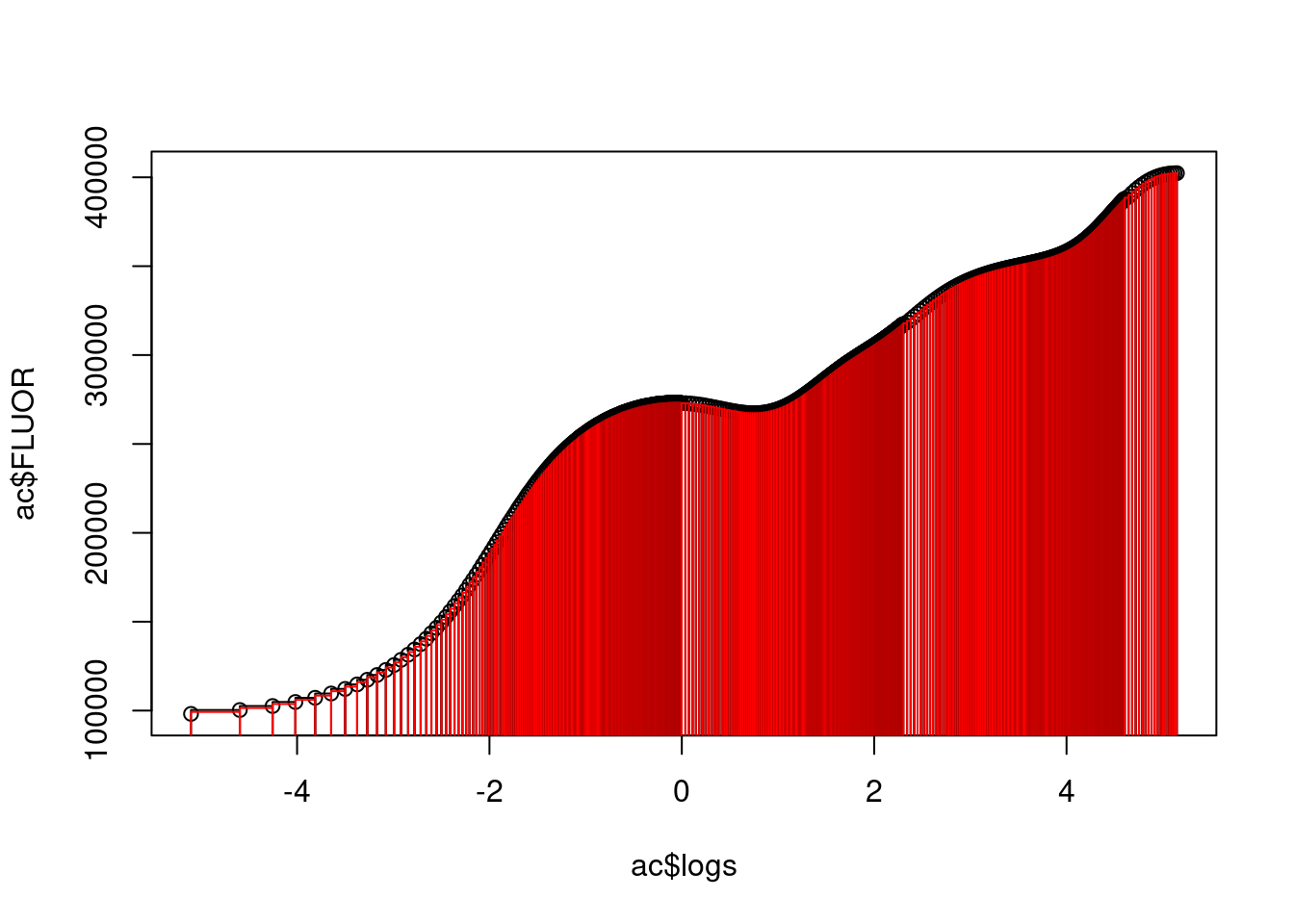
Code
#比较原来数据点的线与使用滚动平均值的线的差异
plot(ac$logs, ac$FLUOR)
for (i in (1:(n-1))){
  rect(ac$logs[i], 0, ac$logs[i+1], ac$FLUOR[i+1])
  rect(ac$logs[i], 0, ac$logs[i+1], roll[i], border = 'red')
}
Figure 20.1: 比较使用简化方式计算面积与原来数据点连线之间的差异

通过 Figure 20.1 我们能够看到，二者差异非常小(黑色是原始测量数据，红色为使用滚动平均值的数据)，即使是些微低估，也是所有的处理都存在这个情况，总比有的样条插值拟合曲线好，有的拟合不好要来得一致一些。而对于标准化之后的面积 Sm，那么小数点后第三位的误差，不会对结果造成明显影响，因为这个面积个位数或者十位数是普遍现象。