23 叶肉导度计算

photosynthesis` 使用了 Harley 等 (1992) 的可变电子流的方式计算 g_m，其文章中对该部分理论进行了详细介绍，在正式开始演示前，我觉得还是有必要简单复述一下其中内容，以便我们理解需要测量的参数以及这个函数的操作。

23.1 理论

从大气中 CO₂ 扩散到叶绿体中分压的下降与每个步骤的导度成反比：

A=(C_a - C_i) \cdot g_s/P = (C_i - C_c) \cdot g_m/P \tag{23.1}

这里 P 指的是大气压。这个关于气体扩散的定理自然是后面计算所需的基石。之所以使用分压，是因为气体扩散经过叶肉细胞时，叶肉细胞内是液相空间，而根据 Henry’s law:

P \propto C (or) P = k_H \cdot C \tag{23.2}

也就是描述气体溶于水的量，与其分压成正比。

而对于 FvCB 模型，我们一般都认为 RuBP 的羧化受到下面三个因子的限制：

Rubisco 的活性，
RuBP 的再生（或者称为为 J 限制），
磷酸丙糖代谢为淀粉或蔗糖时正磷酸盐的释放

当 Rubisco 限制阶段，光合作用的描述是：

A = \frac{V_{cmax} \cdot C_c}{C_c + K_c \cdot (1+O/K_O)} \cdot \bigg(1-\frac{\Gamma^*}{C_c} \bigg) - R_d \tag{23.3}

根据 Henry’s law 替换 C_c：

A = \frac{V_{cmax} \cdot (C_i - A/g_m)}{C_c + K_c \cdot (1+O/K_O)} \cdot \bigg(1-\frac{\Gamma^*}{C_i - A/g_m)} \bigg) - R_d \tag{23.4}

当处于 RuBP 限制阶段时：

A = J \cdot \frac{(C_i - A/g_m) - \Gamma^*}{4 \cdot ((C_i - A/g_m) +2\Gamma^*)} - R_d \tag{23.5}

而电子传递速率可以通过辐射的光量子密度来计算：

J = \frac{0.24 \quad PPFD}{(1+0.24^2 \cdot PPFD^2 / J_{max})^{0.5}} \tag{23.6}

而 RuBP 限制阶段的公式也可以用写为电子传递速率的形式：

J = (A+R_d) \cdot\frac{4 \cdot ((C_i - A/g_m) + 2 \Gamma^*)}{(C_i - A/g_m)-\Gamma^*} \tag{23.7}

观察上面的公式我们可以看到，这个公式的适用性很广。而计算叶肉导度的方法，不管是可变电子流还是恒定电子流，都与其密切相关。

23.2 恒定电子流

恒定电子流的假设是 J 不随 CO₂ 的分压而改变。因而，需要一个荧光二氧化碳响应曲线来确定 J 不随 CO₂ 而变化的范围。一个共识是认为当 PPFD 和其他淬灭参数不变时， J 是恒定的，如果光强小于饱和的 PPFD，很容易得到更广范围的 CO₂ 分压下 J 是否恒定。该方法尽管存在限制，但是他的优势是可以基于多个气体交换的测量进行计算，从而降低单个测量的误差。

23.3 可变电子流

对于可变电子流，只是认为 J 是变化的，但是 J 可以通过叶绿素荧光测量直接获得。

g_m = \frac{A}{C_i - \frac{\Gamma^*[J+ 8 \cdot(A+ R_d)]}{J - 4 \cdot (A + R_d)}} \tag{23.8}

该方法测量相比来说比较简单。

23.3.1 可变电子流的限制因素

恒定电子流可以在一系列大的 CO₂ 跨度下使用，但是要解决 CO₂ 对 g_m 影响的问题，则需要可变电子流的方式。但是可变电子流中参数 R_d，\Gamma^* 存在不确定性，而对 J 的计算错误则导致整个计算错误。因而作者确定了一个通过 C_c 对 (A+R_d) 斜率的阈值进行判定的计算叶肉导度是否合理的方法。因为：

C_c = \Gamma^*[J+8\cdot(A+R_d)]/[J-4 \cdot(A+R_d)] \tag{23.9}

那么：

dC_c/dA = 12 \cdot \Gamma^* \cdot J/[J - 4 \cdot(A+R_d)]^2 \tag{23.10}

最终确认的有限的计算数据必须满足 10 < dC_c/dA < 50。这是 fit_g_mc_variable 所采用的合理的叶肉导度相关列所必须满足的条件。

23.4 函数介绍

Code

fit_g_mc_variableJ(
  data,
  varnames = list(A_net = "A_net", J_etr = "J_etr", C_i = "C_i", PPFD = "PPFD",
    phi_PSII = "phi_PSII"),
  usealpha_Q = FALSE,
  alpha_Q = 0.84,
  beta_Q = 0.5,
  gamma_star,
  R_d,
  P = 100
)

函数本身参数都比较简单。函数有一个计算数据可靠性的检测，并只使用它检测有效的数据进行拟合进行取平均值，而且他计算的单位是按分压计算的：m^{-2} \cdot s^{-1} \cdot Pa^{-1}。

我使用软件包自带的数据进行演示，当然了 LI-6400 也是可以的，但请参考开始的连接中的文章，来进行相应处理，首先是加载软件包，我们顺便看一下数据：

Code

library(photosynthesis)
gm_data <- read.csv("data/A_Ci_Q_data_1.csv")

然后进行拟合就可以了：

Code

data <- fit_g_mc_variableJ(
  gm_data,
  varnames = list(
    A_net = "A",
    J_etr = "ETR",
    C_i = "Ci",
    PPFD = "Qin",
    phi_PSII = "PhiPS2"
  ),
  gamma_star = 46,
  R_d = 0.153,
  usealpha_Q = TRUE,
  alpha_Q = 0.84,
  beta_Q = 0.5,
  P = 84
)

我们可以看一下 data 前的数据，仅显示 gsw 和 g_mc(计算的叶肉导度)：

gsw	g_mc
0.3458193	1.1366292
0.3409737	1.0829398
0.3460976	1.1646861
0.3666962	1.0234578
0.3977929	-0.5338358
0.4284309	0.8689417

可以看到，是有很多不合理值的，我们可以作图看一下合理的值：

Code

ggplot(data, aes(x = CO2_s, y = g_mc, colour = reliable)) +
  labs(x = expression(CO[2]~"("*mu*mol~mol^{-1}*")"),
       y = expression(g[m]~"(mol"~m^{-2}~s^{-1}~Pa^{-1}*")")) +
  geom_point(size = 2) +
  theme_bw() +
  theme(legend.position = 'bottom')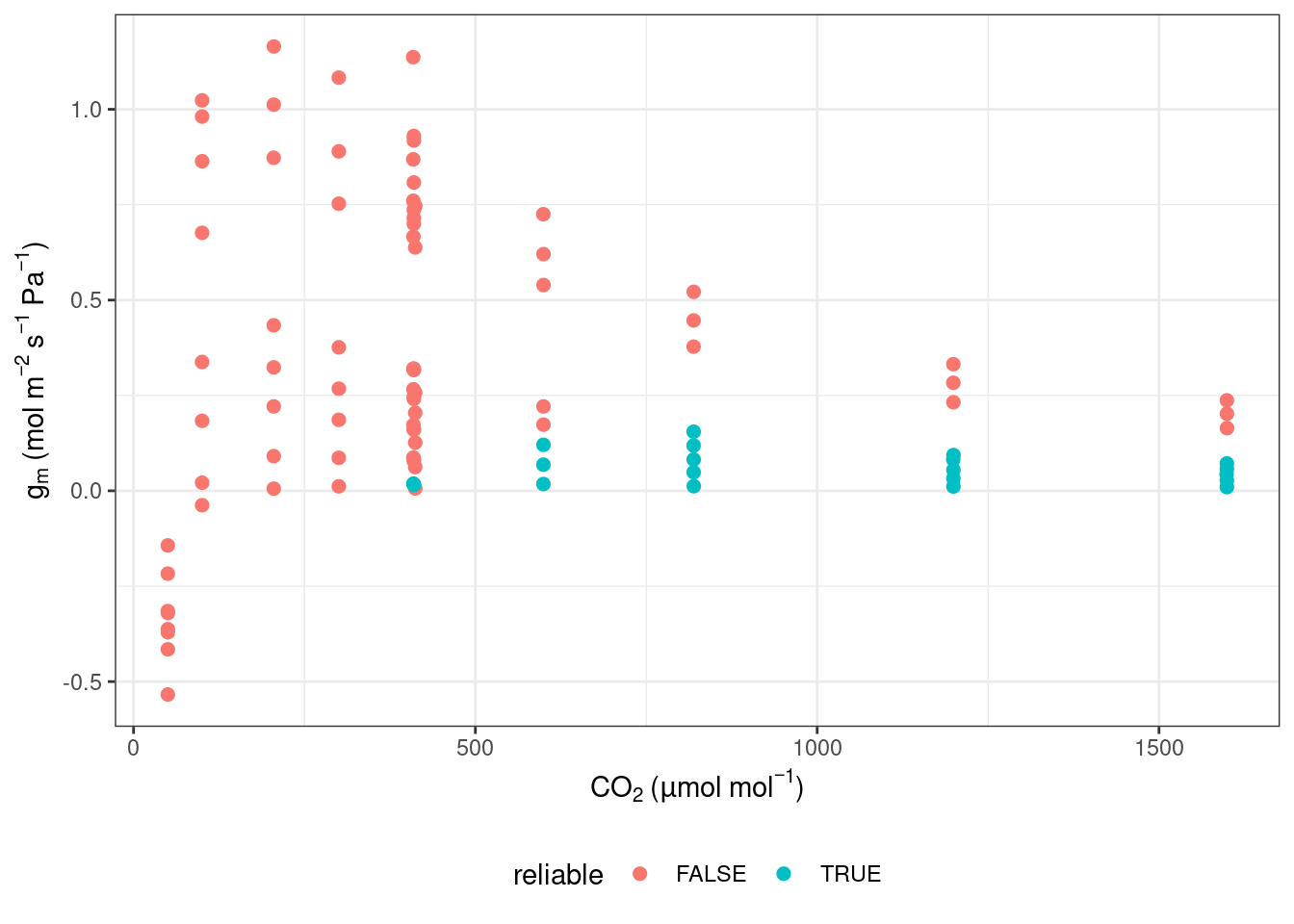

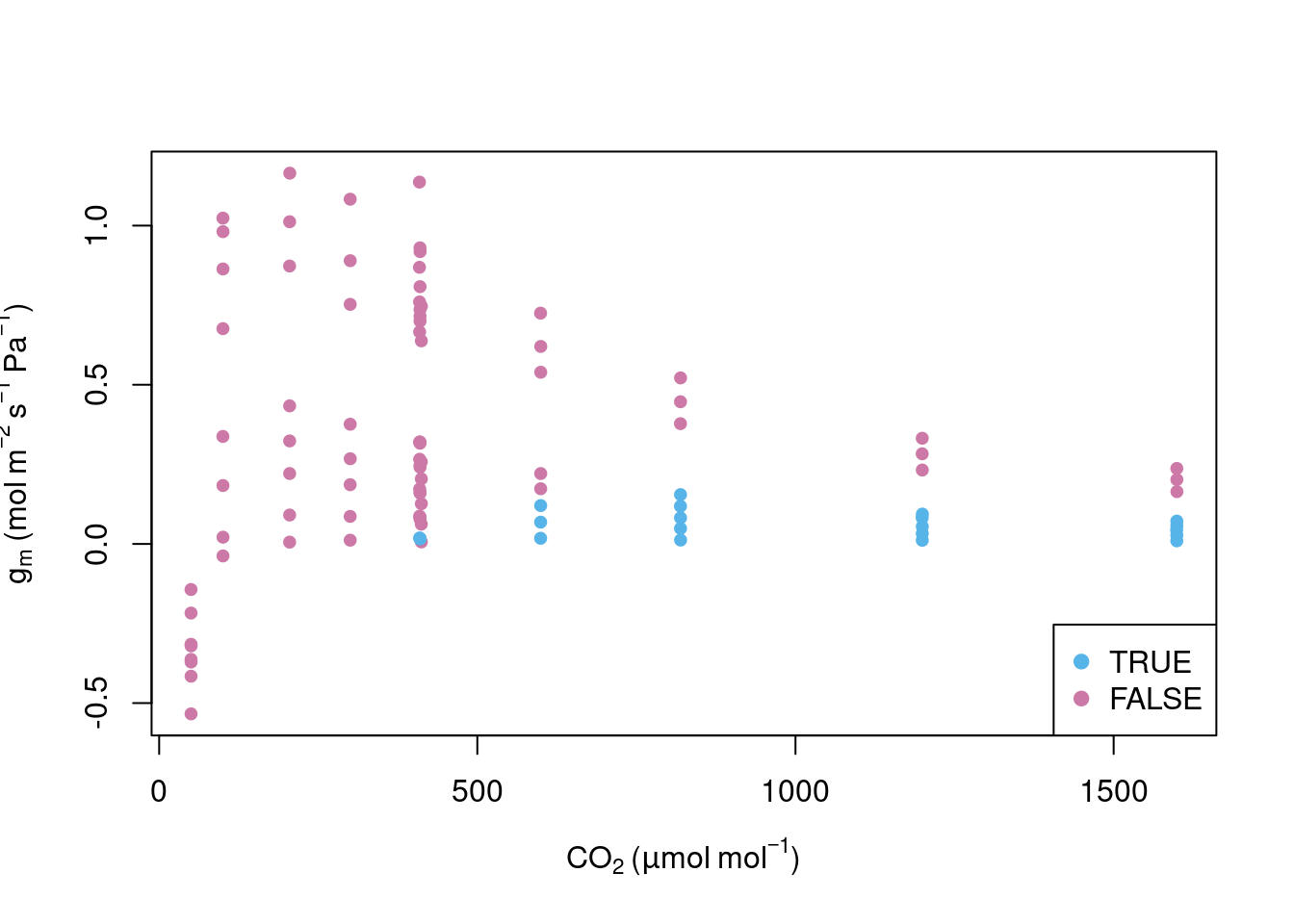
当然上面的作图来自于 vignette，如果与我一样还没赶上潮流，可以使用 base plot：

Code

col_sep <- ifelse(data$reliable == TRUE, "#56B4E9", "#CC79A7")
with(data, {
  plot(CO2_s, g_mc, col = col_sep, 
       xlab = expression(CO[2]~"("*mu*mol~mol^{-1}*")"),
       ylab = expression(g[m]~"(mol"~m^{-2}~s^{-1}~Pa^{-1}*")"),
       pch =19, cex = 0.8)
  legend('bottomright', legend = c('TRUE','FALSE'), pch = 19, col = c("#56B4E9", "#CC79A7"))
})

查看前文所讲的斜率判定相关数据：

Code

#Plot QAQC graph according to Harley et al. 1992
ggplot(data, aes(x = CO2_s, y = dCcdA, colour = reliable)) +
  labs(x = expression(CO[2]~"("*mu*mol~mol^{-1}*")"),
       y = expression(delta*C[c]*"/"*delta*A)) +
  geom_hline(yintercept = 10) +
  geom_point(size = 2) +
  theme_bw() +
  theme(legend.position = 'bottom')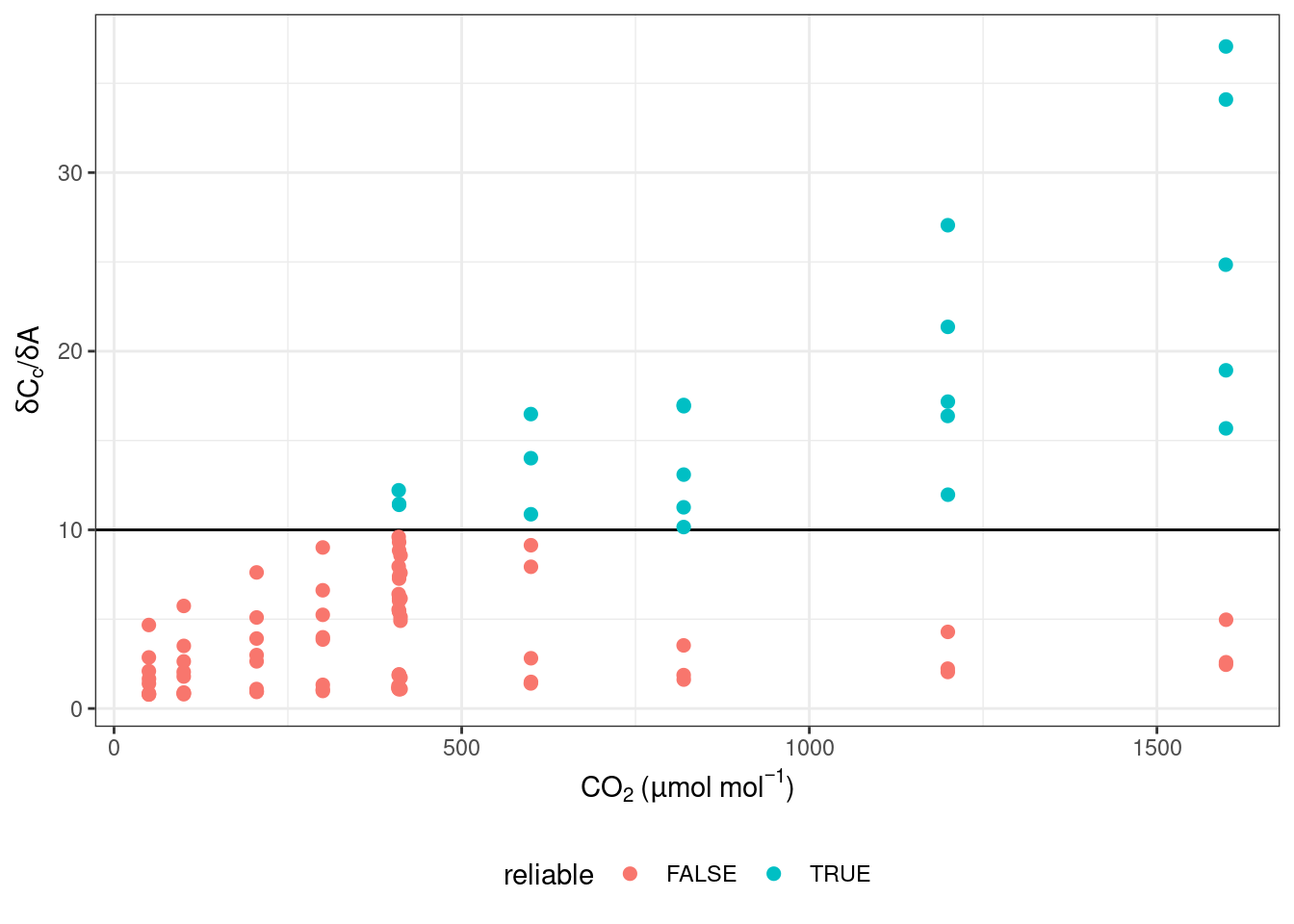

Code

ggplot(data, aes(x = dCcdA, y = g_mc, colour = reliable)) +
  labs(x = expression(delta*C[c]*'/'*delta*A),
       y = expression(g[m]~'(mol'~m^{-2}~s^{-1}~Pa^{-1}*')')) +
  geom_point(size = 2) +
  theme_bw() +
  theme(legend.position = 'bottom')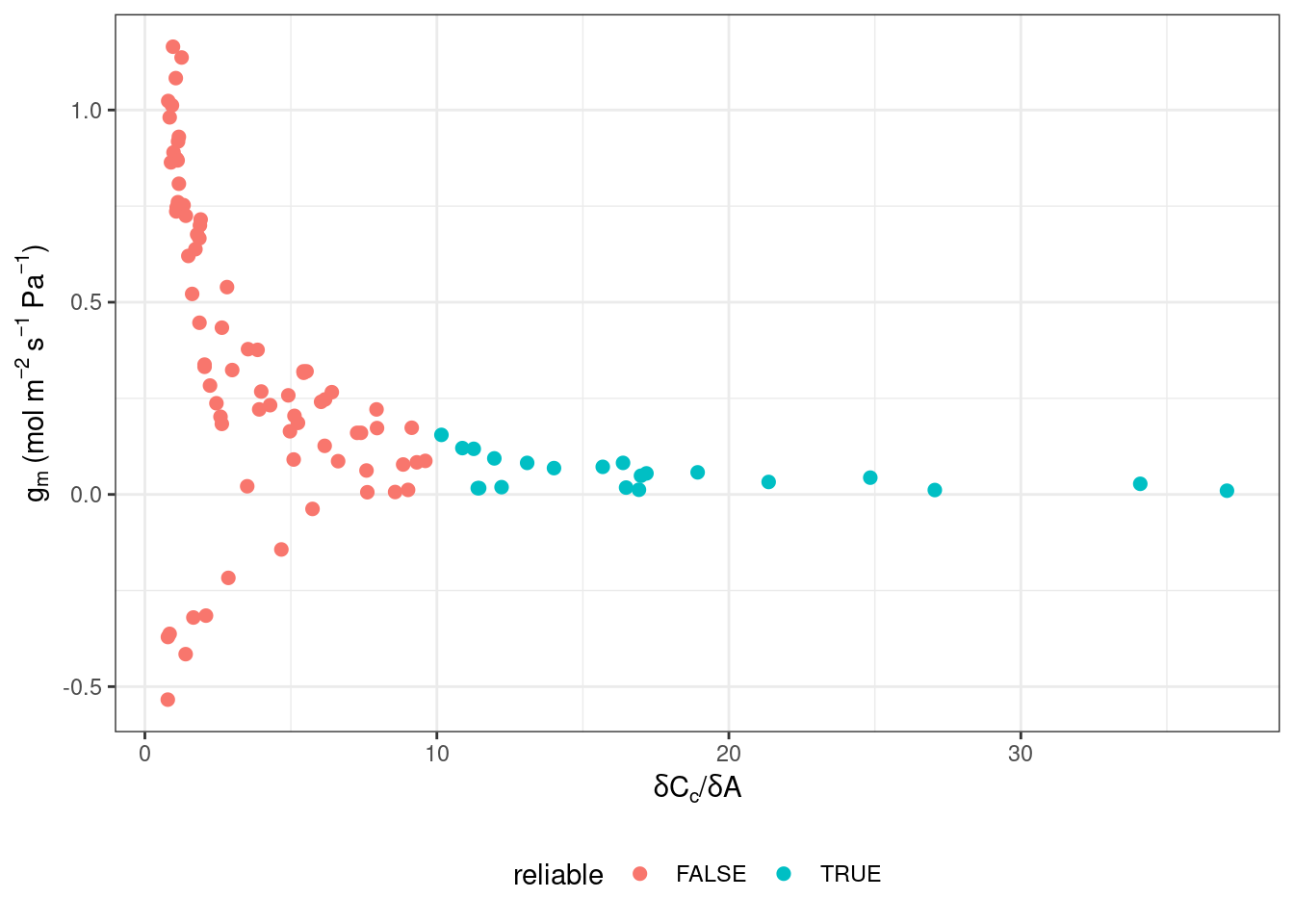

这里数据都已经包含在拟合数据里，想怎么作图可以随意定制。