22  气孔导度模型的拟合

在暂时还没时间多年没时间整理的情况下，先简单记录一下基本操作。

22.1 plantecophys 气孔导度相关函数

22.1.1 fitBB 函数

fitBB(
  data,
  varnames = list(
    ALEAF = "A",
    GS = "gsw",
    VPD = "VPDleaf",
    Ca = "CO2_s",
    RH = "RHcham"
  ),
  gsmodel = c("BBOpti", "BBLeuning", "BallBerry",
              "BBOptiFull"),
  fitg0 = FALSE
)

参数的意义:

• data：待分析的数据文件。
• varnames：注意，函数默认数据为 6400 格式，因此 6800 的数据文件要按照上文的参数修改。 相对湿度只有在使用 BallBerry 时才需要输入。
• gsmodel：上述三个模型之一。
• fitg0：默认不计算g0，若需要，改为TRUE。

代码示例：

library(plantecophys)

aci <- read.csv("data/aci.csv")
aci <- subset(aci, Obs > 0)
fitBB(
  aci,
  varnames = list(
    ALEAF = "Photo",
    GS = "Cond",
    VPD = "VpdL",
    Ca = "CO2S",
    RH = "RH_S"
  ),
  gsmodel = "BBOpti",
  fitg0 = TRUE
)

Result of fitBB.
Model :  BBOpti 
Both g0 and g1 were estimated.

Coefficients:
g0  g1
0.326 -0.992 

For more details of the fit, look at summary(myfit$fit)
To return coefficients, do coef(myfit).
(where myfit is the name of the object returned by fitBB)

22.1.2 fitBBs 函数

如果我们有多个物种或分组的数据，那么使用 fitBBs 则可以快速拟合多条曲线的数据。我们先整合两次的数据，然后来查看一下运行结果：

aci01 <- read.csv("data/aci01.csv")
aci01 <- subset(aci01, Obs > 0)
multiBB <- data.frame(
  A = c(aci$Photo, aci01$Photo),
  GS = c(aci$Cond, aci01$Cond),
  CO2S = c(aci$CO2S, aci01$CO2S),
  VPD = c(aci$VpdL, aci01$VpdL),
  RH = c(aci$RH_S, aci01$RH_S),
  species = c(rep("species1", length(aci$Photo)),
              rep("species2", length(aci01$Photo)))
)

mod2 <- fitBBs(
  multiBB,
  group = "species",
  varnames = list(
    ALEAF = "A",
    GS = "GS",
    VPD = "VPD",
    Ca = "CO2S",
    RH = "RH"
  ),
  gsmodel = "BallBerry",
  fitg0 = TRUE
)

结果为：

coef(mod2)

group	g0	g1
species1	0.3263885	-0.1734554
species2	0.0515873	-0.0218842

22.2 photosynthesis 气孔导度相关函数

22.2.1 无分组模型的实现过程

内容与上面 的重复，这里不在运行，仅列出代码。

读取数据：

library(photosynthesis)
df <- read.csv("data/A_Ci_Q_data_1.csv")

BallBerry 模型需要相对湿度，而 LI-6800 的相对湿度数据实际上是转换为百分数后的数据，因此需要处理一下，然后这个函数的方便之处是，它可以一次拟合出所有的模型来：

df$RH <- df$RHcham / 100

fits <- fit_gs_model(
  data = df,
  varnames = list(
    A_net = "A",
    C_air = "Ca",
    g_sw = "gsw",
    RH = "RH",
    VPD = "VPDleaf"
  ),
  model = c("BallBerry",
            "Leuning",
            "Medlyn_partial",
            "Medlyn_full"),
  D0 = 3
)

函数的参数其实都比较简单，如果对非线性拟合不满意，也可以传入 nlsLM 的参数。

结果的查看

fit_gs_model 结果有两个水平，第一层 list 是拟合模型，第二层则是模型相关的参数、图形等，可以通过位置查看：

fits[[1]][1]
fits[[1]][2]
fits[[1]][3]

也可以通过名称查看：

fits$BallBerry$Parameters
fits$Leuning$Graph
fits$Medlyn_partial$Parameters
fits$Medlyn_full$Parameters

22.2.2 分组模型的实现

分组数据处理起来也比较方便，例如下面以光强为分组，photosynthesis 提供了两个方便的函数，帮助进行分组数据的操作，fit_many 用于选择函数用于分组数据，compile_data 用于将 list 结果转为 dataframe：

df$Q_2 <- as.factor(round(df$Qin, digits = 0))

fits <- fit_many(
  df,
  varnames = list(
    A_net = "A",
    C_air = "Ca",
    g_sw = "gsw",
    RH = "RH",
    VPD = "VPDleaf"
  ),
  funct = fit_gs_model,
  group = "Q_2"
)

数据的查看比之前又多了一个水平，例如 750 光强下的数据：

fits[["750"]][["Medlyn_partial"]][["Parameters"]]

这里转换过程分两部，首先是将所有的参数转为 list 形式，转换对象是 1，也就是第一个模型 BallBerry。然后再将这个 list 进行一次转换，不同分组的参数 Parameters（顺序可参考未分组数据的结果）：

bbmods <- compile_data(data = fits,
                     output_type = "list",
                     list_element = 1)
bbpars <- compile_data(data = bbmods,
                     output_type = "dataframe",
                     list_element = 2)

bbpars$ID <- as.numeric(bbpars$ID)

plot(g0 ~ ID, bbpars)

最后展示的图形是不同光强下，拟合的截距的差异。多个图形也可以使用这种方式转换，不过存储的类型最好是 list（存储的是 ggplot2 对象的类）。例如 vignette 使用下面的方式查看第三幅图的结果。

graphs <- compile_data(data = bbmods,
                       output_type = "list",
                       list_element = 3)

graphs[[3]]

22.3 光合最优气孔导度耦合模型

Cowan 和 Farquhar (1977) 关于最优气孔导度的描述概括如下： 最优气孔行为理论认为气孔的最优化行为，指的是在某一时间段内， 最大化的进行光合碳固定的同时最小化的进行蒸腾作用，也就是说，对于一定的水分消耗，得到最大化的光合碳固定。即使得：

A - \lambda E \tag{22.1}

最大化，其中 \lambda 是临界水分利用效率，也即植物损耗单位水分的 C 生产量，单位一般为 mol \: CO_2 \cdot mol^{-1} H_2O，可通过光合速率和蒸腾速率的比值计算。plantecophys 包含了相关的函数来处理。

22.3.1 FARAO 函数

FARAO 函数用于找到最大化 A - \lambda E 解的** Ci **值，这里是利用数值解的形式求解方程。

FARAO(lambda = 0.002, Ca = 400, VPD = 1,
      photo = c("BOTH", "VCMAX","JMAX"), 
      energybalance = FALSE, C4 = FALSE, 
      Tair = 25, Wind = 2, Wleaf = 0.02,
      StomatalRatio = 1, LeafAbs = 0.86, ...)

FARAO2(lambda = 0.002, Ca = 400, 
       energybalance = FALSE, ...)

其参数同 fitaci 和 Photosyn，在此不多做介绍，FARAO 使用的是 Cowan 和 Farquhar (1977) 的方法得到最优化的 Ci 值, FARAO2 则更简单或可能更稳定，利用 Buckley 等 (2014) 的方法来计算, Medlyn 等 (2011) 的方法是这个数值解的近似值。

22.4 光合气孔导度耦合模型

Remko A. Duursma (2015) 对于气体交换耦合模型的简述如下：

• 对于 FvCB 模型有：

A_n = min(A_c, A_j)-R_d \tag{22.2}

• 在假定 gm 为恒定的前提下：

C_c = C_i - \frac{A_n}{g_m} \tag{22.3}

• 根据 Ficker 定理

A_n = \frac{g_s}{1.6}(C_a - C_i) \tag{22.4}

以及 BallBerry 气孔导度模型 g_s = g_0 + g_1 \frac{A_n}{C_a} f(D) \tag{22.5}

整合公式 公式  22.2, 公式  22.3, 公式  22.4 和 公式  22.5 后得到气体交换的耦合模型，气体交换耦合模型有很多更大尺度上的应用，例如 R. A. Duursma 和 Medlyn (2012) 和 wang1998a，可用于预测 An，gs 和蒸腾速率对主要环境驱动因子的响应（除土壤水分），并包含了主要的叶片性状（g1，V_cmax, J_max, R_d 以及他们的温度依赖性）。

22.4.1 Photosyn 函数

Photosyn 为耦合的光合–气孔导度模型，基于 Farquhar 光合模型和 Ball-Berry 气孔导度模型。

Photosyn(VPD = 1.5, Ca = 400, PPFD = 1500,
         Tleaf = 25, Patm = 100,RH = NULL,
         gsmodel = c("BBOpti", "BBLeuning", 
                     "BallBerry", "BBdefine"),
         g1 = 4, g0 = 0, gk = 0.5, vpdmin = 0.5,
         D0 = 5, GS = NULL, BBmult = NULL, 
         alpha = 0.24, theta = 0.85, Jmax = 100,
         Vcmax = 50, gmeso = NULL, TPU = 1000, 
         alphag = 0, Rd0 = 0.92, Q10 = 1.92,
         Rd = NULL, TrefR = 25, Rdayfrac = 1, 
         EaV = 82620.87, EdVC = 0, delsC = 645.1013, 
         EaJ = 39676.89, EdVJ = 2e+05, delsJ = 641.3615,
         GammaStar = NULL, Km = NULL, Ci = NULL, 
         Tcorrect = TRUE,returnParsOnly = FALSE,
         whichA = c("Ah", "Amin", "Ac", "Aj"))

Aci(Ci, ...)

因为是光合气孔导度模型的耦合，故而参数与之前的函数相同，参见 sec. 22.1.1 和 章节 15 部分的内容。

Photosyn 使用举例

library(plantecophys)
# 仅使用下面几个参数运行模型
#（其他参数使用默认值）
# 利用已测量或计算的参数
Photosyn(VPD=2, g1=4, Ca=500)

        Ci    ALEAF        GS    ELEAF       Ac       Aj   Ap   Rd VPD Tleaf
1 369.3981 14.19466 0.1706377 3.412753 15.12654 17.03685 1000 0.92   2    25
   Ca       Cc PPFD Patm
1 500 369.3981 1500  100

# 部分参数相同，而某一参数或某几个参数不同时，
# 可以将不同的参数设置为一个序列（vectors）
r <- Photosyn(VPD=seq(0.5, 4, length=25), 
              Vcmax=50, Jmax=100)
with(r, plot(VPD, ALEAF, type='l'))

Figure 22.1: VPD VS. An

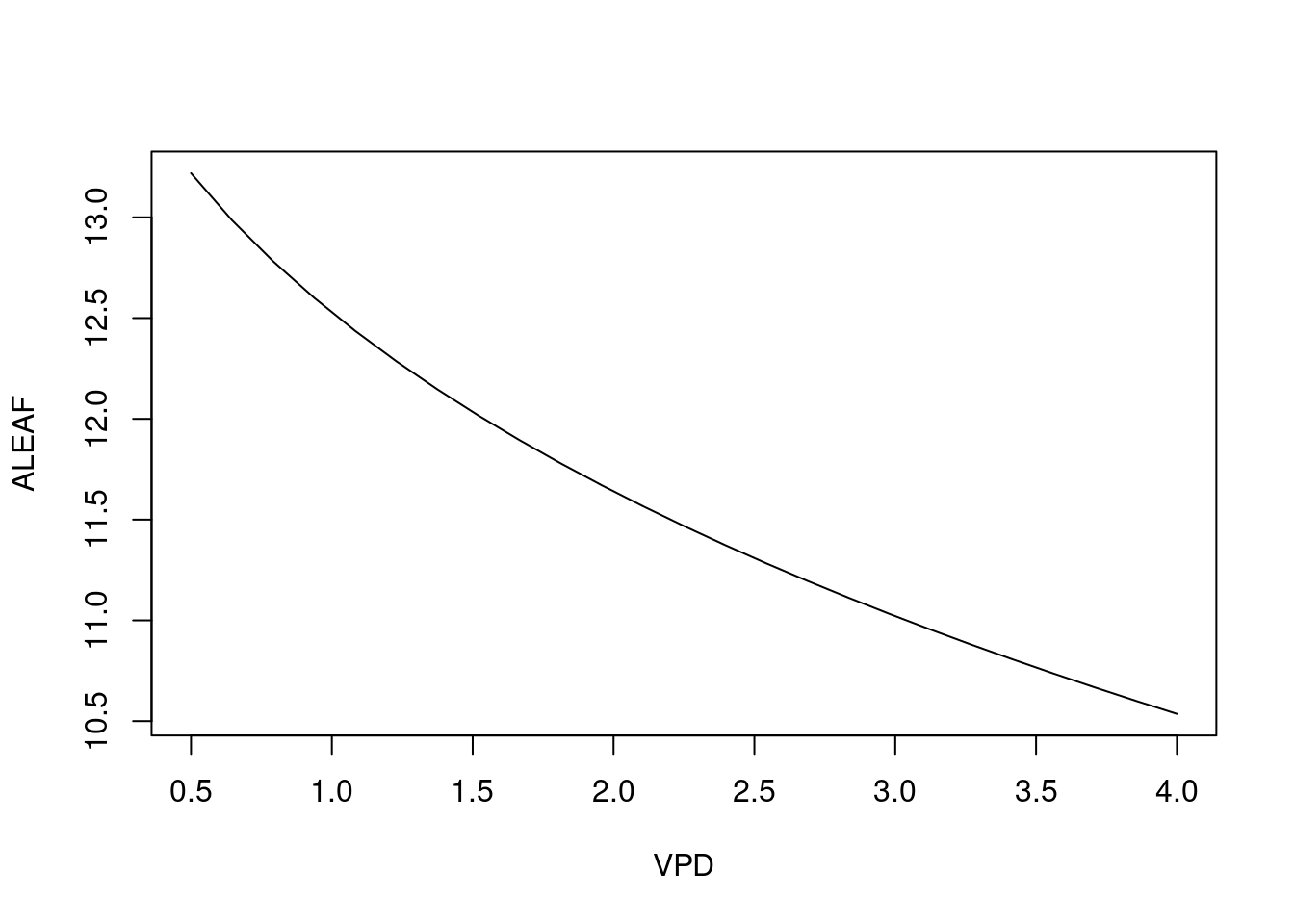
Figure 22.1 显示了不同 VPD 下的光合速率。

# 设定叶肉导度的拟合
run1 <- Photosyn(PPFD=seq(50,1000,length=25), 
                 gmeso=0.15, Vcmax=40, Jmax=85)
with(run1, plot(PPFD, GS, type='l'))

PPFD VS. GS

# 运行ACi曲线数据（提供Ci值而不是计算）
arun1 <- Aci(Ci=seq(50, 1200, length=101), 
             Vcmax=40, Jmax=85)
arun2 <- Aci(Ci=seq(50, 1200, length=101), 
             Vcmax=30, Jmax=70)
with(arun1, plot(Ci, ALEAF, type='l'))
with(arun2, points(Ci, ALEAF, type='l', lty=5))

PPFD VS. GS

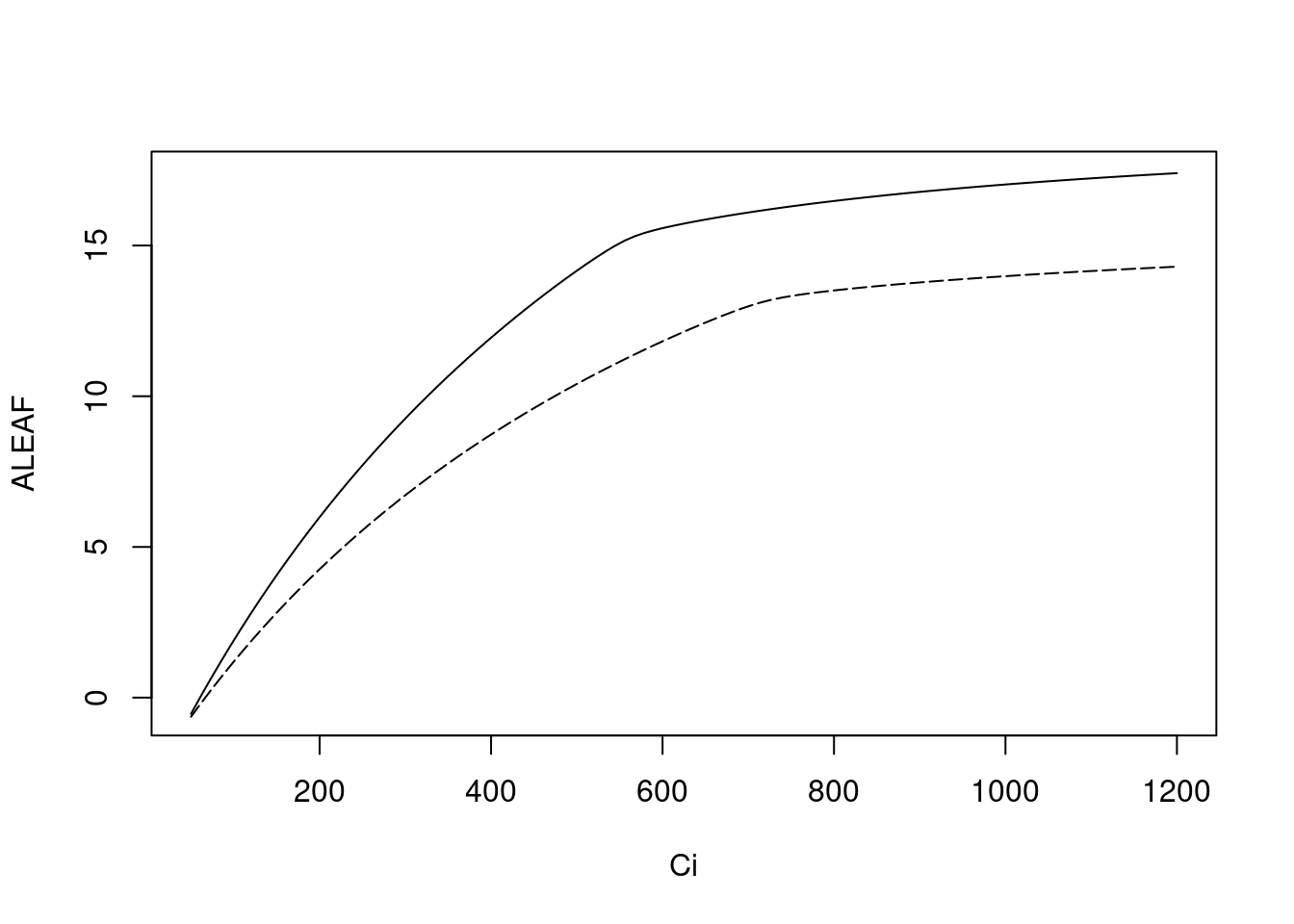
?fig-ppfd 显示不同 C_i 下的光合速率。

# 找出CO2需求和供给的交叉点
# 设定部分参数
gs <- 0.2 # 对水的气孔导度
Ca <- 400 # 外部CO2
gctogw <- 1.57 # 转换系数
gc <- gs / gctogw # 对 CO2 的气孔导度
# 需求曲线
p <- Aci(seq(60,500,length=101), Ca=400)
# 提供气孔导度及交叉点
g <- Photosyn(GS=gs, Ca=Ca)
# 交叉点可视化
par(yaxs="i")
with(p, plot(Ci, ALEAF, type='l', 
             ylim=c(0,max(ALEAF))))
with(g, points(Ci, ALEAF, pch=19, col="red"))
abline(gc * Ca, -gc, lty=5)
legend("topleft", c(expression(
  "Demand:"~~A==f(C[i])),
   expression("Supply:"~~A==g[c]*(C[a]-C[i])),
              "Operating point"),
   lty=c(1,5,-1),pch=c(-1,-1,19),
   col=c("black","black","red"),
   bty='n', cex=0.9)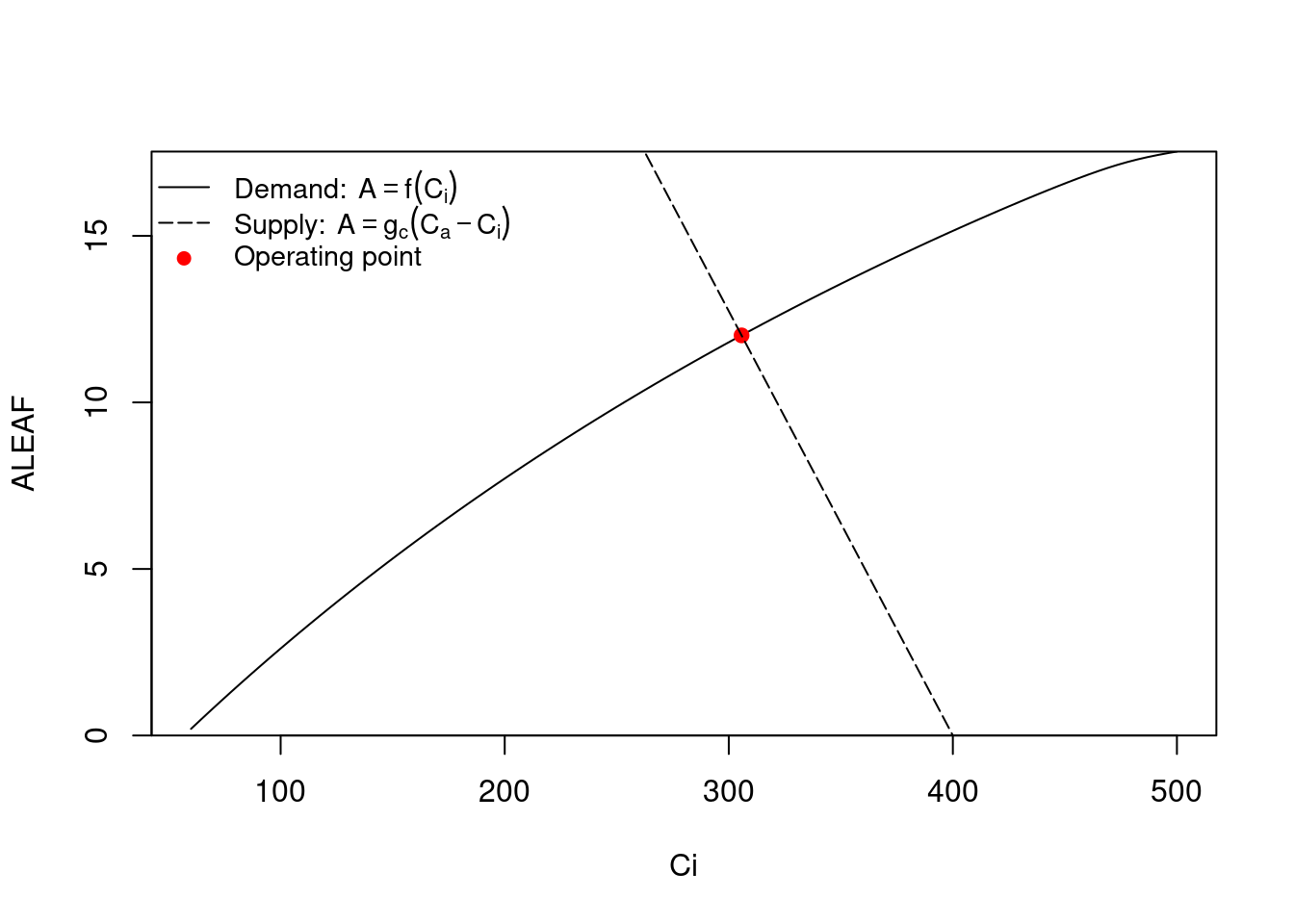

Figure 22.2: supply VS. demand

Figure 22.2 需求与供给的关系。

22.4.2 PhotosynEB 函数

使用同 Photosyn，只不过使用能量平衡法来计算叶温。

警告

目前版本尚存在bug，不能直接提供 GS 来计算，否则会出现未知错误。

22.4.3 PhotosynTuzet 函数

同样为光合气孔导度耦合模型，只不过基于 Tuzet, Perrier, 和 Leuning (2003) 的气孔导度模型，现将其描述如下：

g_{co2} = g_0 + \frac{a A}{C_i - \Gamma} f_{\Psi v} \tag{22.6}

其中 g_co2 为对 CO₂ 的气孔导度， g₀ 是残余导度（residual conductance）(在补偿点时限制 g_CO2 的值）， A 为光合速率，C_i 为胞间二氧化碳浓度，\Gamma 为 CO₂ 补偿点，a 是经验系数。

一个根据经验的逻辑方程用于描述气孔对水势的敏感性：

f_{\Psi v} = \frac{1 + exp(s_f \Psi_f)}{1 + exp(s_f(\Psi_f - \Psi_v))} \tag{22.7}

\Psi_v 是指叶片水势，\Psi_f 是参比势能， 该方程假设在水势接近于 0 时，气孔对叶片水势不敏感，并且气孔随着 \Psi_v 的下降快速关闭。\Psi_f 和 s_f (曲线形状参数) 依赖于不同物种的形态学适应以及生长过程中所处的环境。

PhotosynTuzet 的参数

除 Tuzet, Perrier, 和 Leuning (2003) 模型中使用的参数外，其他参数都继承了 Photosyn 的参数

PhotosynTuzet(g1 = 8, Ca = 400, psis = 0,
              kl = 2, sf = 3, psif = -2,
...)

• g1：斜率参数，要远比 fitBB 中的大。
• Ca：外界大气 CO₂ 浓度
• psis，土壤水势（Mpa）。
• kl：Leaf-specific hydraulic conductance（叶片导水参数 (mmol \cdot m^{-2} \cdot s^{-1} \cdot MPa^{-1})，叶片蒸腾量、叶片面积及叶片水势计算）。
• sf：曲线形状参数。
• 在气孔导度为最大值 50% 时的叶片水势。

Buckley, T. N., S Martorell, A Diazespejo, M Tomàs, 和 H Medrano. 2014. 《Is stomatal conductance optimized over both time and space in plant crowns? A field test in grapevine Vitis vinifera.》 Plant Cell & Environment 37 (12): 2707.

Cowan, I. R., 和 G. D. Farquhar. 1977. 《Stomatal function in relation to leaf metabolism and environment.》 Symposia of the Society for Experimental Biology 31 (23): 471.

Duursma, R. A., 和 B. E. Medlyn. 2012. 《MAESPA: a model to study interactions between water limitation, environmental drivers and vegetation function at tree and stand levels, with an example application to CO_2 drought interactions》. Geoscientific Model Development Discussions 5 (4): 919–40.

Duursma, Remko A. 2015. 《Plantecophys-An R Package for Analysing and Modelling Leaf Gas Exchange Data》. Plos One 10 (11): e0143346.

Medlyn, Belinda E., Remko A. Duursma, Derek Eamus, David S. Ellsworth, I. Colin Prentice, Craig V. M. Barton, Kristine Y. Crous, Paolo De Angelis, Michael Freeman, 和 Lisa Wingate. 2011. 《Reconciling the optimal and empirical approaches to modelling stomatal conductance》. Global Change Biology 17 (6): 2134–44.

Tuzet, A, A Perrier, 和 R Leuning. 2003. 《A coupled model of stomatal conductance, photosynthesis and transpiration》. Plant Cell and Environment 26 (7): 1097–1116.