10 指数模型

光合指数模型较多，我们此处使用的指数模型为 Prado 和 Moraes (1997)，其表达式为：

P_{n} = P_{nmax}[1 - e^{-b(I-I_{C})}] \tag{10.1}

其中，I_{c} 为光补偿点，e 为自然对数的底，b为常数，其他参数意义同公式 10.1。同样，该方程仍然是没有极值的函数，但我们可以直接求得光补偿点。

10.1 指数模型的实现

Code

library(minpack.lm)

# 读取数据，同fitaci数据格式
lrc <- read.csv("data/lrc.csv")
lrc <- subset(lrc, Obs > 0)

# 光响应曲线没有太多参数，
# 直接调出相应的光强和光合速率
# 方便后面调用
lrc_Q <- lrc$PARi
lrc_A <- lrc$Photo 

# 模型的拟合
lrcnls <- nlsLM(lrc_A ~ Am*(1-exp((-b)*(lrc_Q-Ic))),
                start=list(Am=(max(lrc_A)-min(lrc_A)),
                           Ic=5, b=1)
                )
fitlrc_exp <- summary(lrcnls)

# 光饱和点
Isat <- function(Isat){fitlrc_exp$coef[1,1]*
    (1-exp((-fitlrc_exp$coef[3,1])*(Isat-
    fitlrc_exp$coef[2,1])))-0.9*fitlrc_exp$coef[1,1]}

uniroot(Isat, c(0,2000))$root

[1] 558.6038

Code

## 拟合图形
library(ggplot2)
light <- data.frame(lrc_Q = lrc$PARi, lrc_A = lrc$Photo)

exp_form <- y ~ Am*(1-exp((-b)*(x -Ic)))

ggplot(light, aes(x = lrc_Q, y = lrc_A)) + 
  geom_point(shape = 16, size = 3, color = "green") + 
  geom_smooth(method="nls", formula = exp_form, 
    se = FALSE, method.args = list(
    start = c(Am=(max(lrc_A)-min(lrc_A)),
    Ic=5, b=0.002), aes(x =lrc_Q, y = lrc_A, 
    color='blue', size = 1.2))
  )  +
  labs(y=expression(paste("photosynthetic rate  ", 
          "(", mu, mol%.%m^-2%.%s^-1, ")")), 
       x=expression(paste("PAR ", 
           "(", mu, mol%.%m^-2%.%s^-1, ")"))) +
  theme_light()

Table 10.1: 指数模型计算参数

	Estimate	Std. Error	t value	Pr(>\|t\|)
Am	13.6547568	0.1723363	79.233185	0.0000000
Ic	-0.5133438	2.3370250	-0.219657	0.8305573
b	0.0041183	0.0002012	20.467032	0.0000000

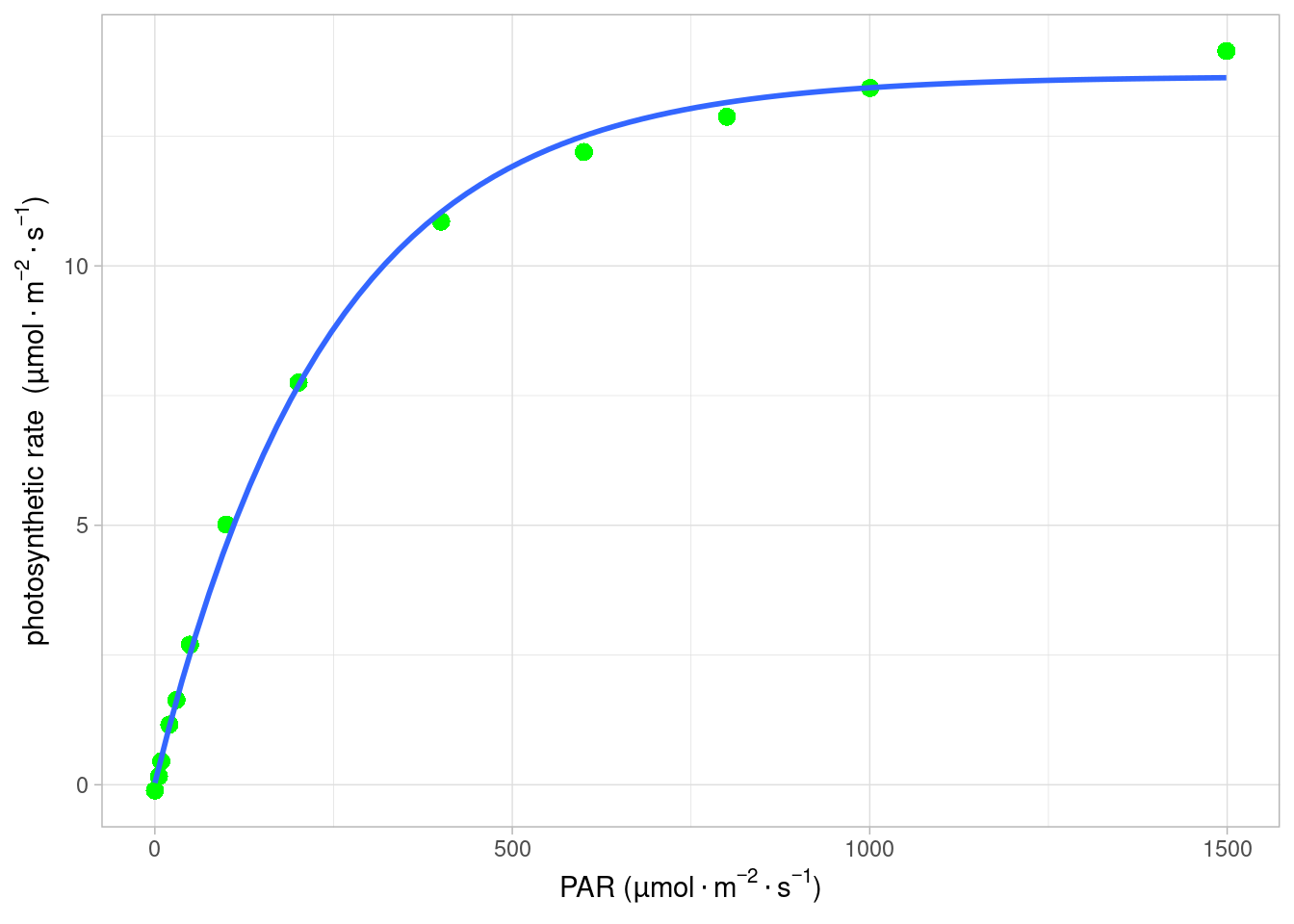
最终的数据拟结果如图 Figure 10.1 所示，拟合的参数及结果见表 Table 10.1。