12 如何选择合适的模型

实际工作中，其实经常遇到有人问选择哪个模型，这个问题简单点的回答就是所有的都试一遍，再看看哪个更合适，但是比较好的做法当然是要通过统计上的验证和根据植物生理来判断，生理上判断比较好解决，拟合参数是不是合适，对于做了一个季节实验的我们来讲，那是相当简单，那统计上的判定呢？那有下面几种方式可供参考。

12.1 AIC 与 BIC

AIC 和 BIC 都是用于模型选择的标准¹，其中他们主要的差别是：

其中 AIC 主要应用目的是，对于给定数据集的多个模型，判定哪个模型对该数据集最合适，该值越小越合适。

而 BIC 的主要目的是对于不同数量拟合参数的模型来选择。同样，该值是越小越好。

但需要注意，如果样本数量过低，那么就需要使用修正的 AIC 指数 (Fabozzi 等 2014)，即 AICc，这个函数不在 base 中，需要第三方的软件包，例如 AICcmodavg。

install.packages('AICcmodavg')

为方便，我们使用 nlsLM 来进行四种模型的比较：

Code

library(minpack.lm)
library(AICcmodavg)

# 读取数据，同fitaci数据格式
lrc <- read.csv("data/lrc.csv")
lrc <- subset(lrc, Obs > 0)

# 光响应曲线没有太多参数，
# 直接调出相应的光强和光合速率
# 方便后面调用
lrc_Q <- lrc$PARi
lrc_A <- lrc$Photo 

# 非直角双曲线模型的拟合
non_rec_aq <- nlsLM(lrc_A ~ 
                (1/(2*theta))*
                (alpha*lrc_Q+Am-sqrt((alpha*lrc_Q+Am)^2 - 
                4*alpha*theta*Am*lrc_Q))- Rd,
                start=list(Am=(max(lrc_A)-min(lrc_A)),
                alpha=0.05,Rd=-min(lrc_A),theta=1)) 
# 直角双曲线
rec_aq <- nlsLM(lrc_A ~ (alpha * lrc_Q * Am) * 
                (1/(alpha * lrc_Q + Am)) - Rd,  
              start=list(Am=(max(lrc_A)-min(lrc_A)),
              alpha=0.05,Rd=-min(lrc_A))
)

# 指数模型的拟合
exp_aq <- nlsLM(lrc_A ~ Am*(1-exp((-b)*(lrc_Q-Ic))),
                start=list(Am=(max(lrc_A)-min(lrc_A)),
                           Ic=5, b=1)
                )

# 直角双曲线修正模型的拟合
mod_rec_aq <- nlsLM(lrc_A ~ alpha * ((1 - 
              beta*lrc_Q)/(1 + gamma * lrc_Q)) * lrc_Q - Rd,
                start=list(alpha = 0.07, beta = 0.00005,
                           gamma=0.004, Rd = 0.2)
                )

AIC(rec_aq, non_rec_aq, exp_aq, mod_rec_aq)

           df        AIC
rec_aq      4  -9.142650
non_rec_aq  5 -27.611987
exp_aq      4   7.099285
mod_rec_aq  5 -19.268459

Code

BIC(rec_aq, non_rec_aq, exp_aq, mod_rec_aq)

           df        BIC
rec_aq      4  -6.882852
non_rec_aq  5 -24.787240
exp_aq      4   9.359083
mod_rec_aq  5 -16.443712

对于 AICc 使用则略微麻烦，因为它没有直接支持向量化操作：

Code

lapply(list(rec_aq, non_rec_aq, exp_aq, mod_rec_aq), AICc)

[[1]]
[1] -4.14265

[[2]]
[1] -19.04056

[[3]]
[1] 12.09929

[[4]]
[1] -10.69703

我们可以看到，结果里出现了负数，这是合理的，我们所讲的越小越好，没有说必须是正直，负值是合理的，而且是常见的。

12.2 方差分析

这个经典方法常常因为就在眼前而让人忽视，实际上他也是可以的，看看 R 是怎么描述 anova 的：

Compute analysis of variance (or deviance) tables for one or more fitted model objects.

当然了，过程很简单:

Code

anova(rec_aq, non_rec_aq, exp_aq, mod_rec_aq)

Analysis of Variance Table

Model 1: lrc_A ~ (alpha * lrc_Q * Am) * (1/(alpha * lrc_Q + Am)) - Rd
Model 2: lrc_A ~ (1/(2 * theta)) * (alpha * lrc_Q + Am - sqrt((alpha * lrc_Q + Am)^2 - 4 * alpha * theta * Am * lrc_Q)) - Rd
Model 3: lrc_A ~ Am * (1 - exp((-b) * (lrc_Q - Ic)))
Model 4: lrc_A ~ alpha * ((1 - beta * lrc_Q)/(1 + gamma * lrc_Q)) * lrc_Q - Rd
  Res.Df Res.Sum Sq Df   Sum Sq F value    Pr(>F)    
1     10    0.20360                                  
2      9    0.04217  1  0.16144  34.458 0.0002377 ***
3     10    0.71020 -1 -0.66803 142.588 8.030e-07 ***
4      9    0.08011  1  0.63009  70.787 1.477e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

不管是从残差的平方和还是 p 值上看，都与 AIC 和 BIC 结果一致。

12.3 肉眼判断

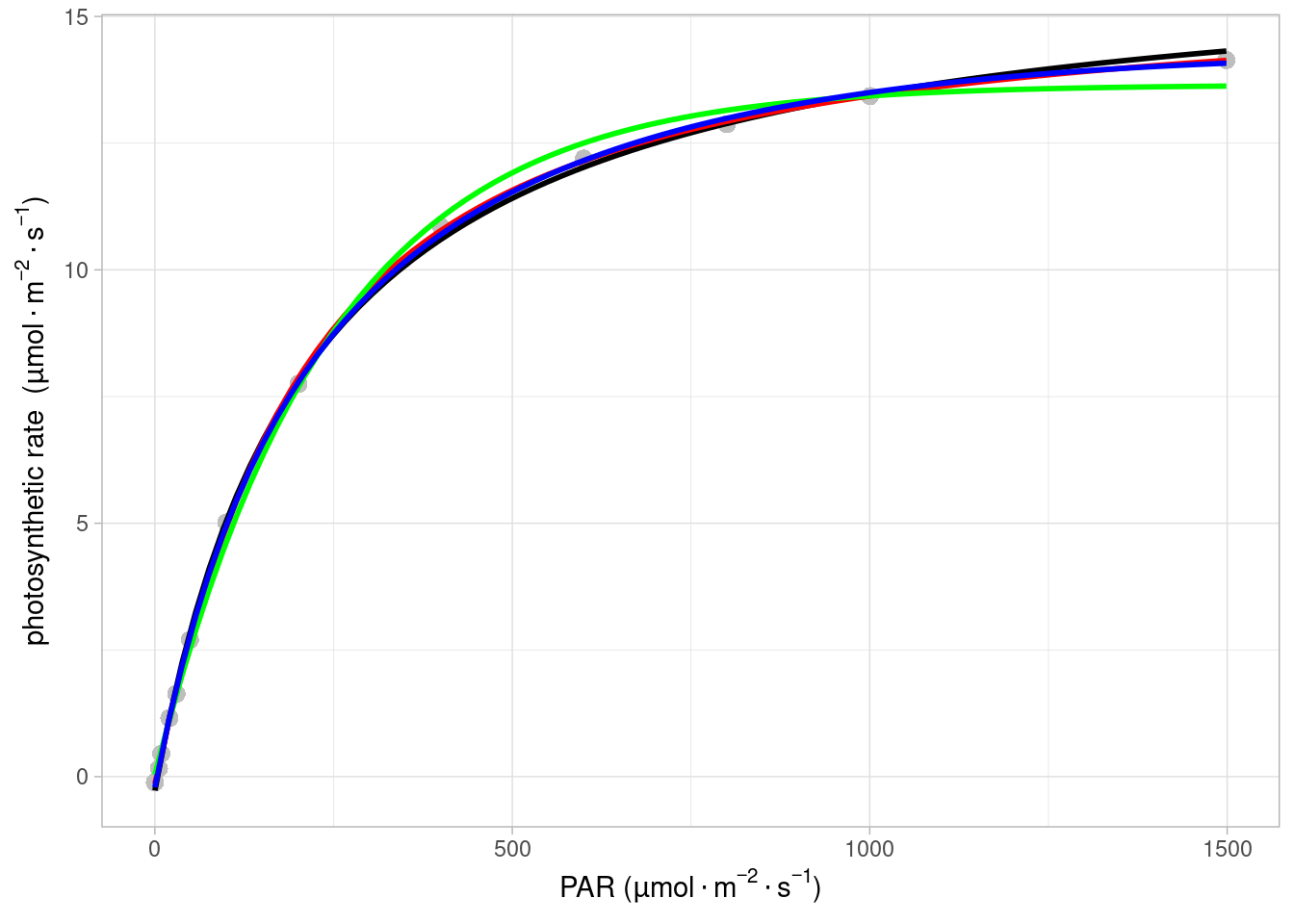
标题有点搞笑，但其实是可以快速筛选判断的，只不过文章里面或附录里面才需要上面的方法来提供数据支持。例如我们把前面几个方程作图的代码整合在一起看一下数据的情况：

Code

library(ggplot2)

# 直角双曲线
rectangular <- y ~ (alpha * x * Am) * (1/(alpha * x + Am)) - Rd
# 非直角双曲线
non_rectangular <- y ~ 
  (1/(2*theta))*(alpha*x+Am-sqrt((alpha*x+Am)^2 - 
   4*alpha*theta*Am*x))- Rd

# 指数模型
exponential <- y ~ Am*(1-exp((-b)*(x -Ic)))

# 修改模型

rectangular_revised <-  y ~ 
  alpha * ((1 - beta*x)/(1 + gamma * x)) * x - Rd

ggplot(lrc, aes(x = lrc_Q, y = lrc_A)) + 
  geom_point(shape = 16, size = 3, color = "gray")+
  
  geom_smooth(method="nls", formula = rectangular, 
              se = FALSE, color='black',
  method.args = list(start = c(
  Am = (max(lrc_A) - min(lrc_A)),
  alpha = 0.05,
  Rd = -min(lrc_A)),
  aes(x =lrc_Q, y = lrc_A, 
   size = 0.9))
  )  +
  
  geom_smooth(method="nls", formula = non_rectangular, 
              se = FALSE, color='red', 
  method.args = list(start = c(Am=(max(lrc_A)-min(lrc_A)), 
  alpha=0.05, Rd=-min(lrc_A), theta=1), 
  aes(x =lrc_Q, y = lrc_A, size = 1.2))) +
                
  geom_smooth(method="nls", formula = exponential, 
    se = FALSE,  color='green',
    method.args = list(
    start = c(Am=(max(lrc_A)-min(lrc_A)),
    Ic=5, b=0.002), aes(x =lrc_Q, y = lrc_A, 
    size = 0.9))
  )+
      
  geom_smooth(method="nls", 
    formula = rectangular_revised,  color='blue',
    se = FALSE, method.args = list(
    start = c(alpha = 0.07, beta = 0.00005,
              gamma=0.004, Rd = 0.2), 
    aes(x =lrc_Q, y = lrc_A, 
    size = 0.9))
  ) + 
  labs(y=expression(paste("photosynthetic rate  ", 
          "(", mu, mol%.%m^-2%.%s^-1, ")")), 
       x=expression(paste("PAR ", 
           "(", mu, mol%.%m^-2%.%s^-1, ")")))+
  theme_light()

该例子并不是特别典型，但结果上来看，红线和蓝线，也就是非直角双曲线和直角双曲线修改模型，看上去比较符合变化趋势。

https://www.rhumbarlv.com/what-does-aic-and-bic-mean/#:~:text=AIC%20means%20Akaike%E2%80%99s%20Information%20Criteria%20and%20BIC%20means,parameters.%20Do%20you%20want%20higher%20or%20lower%20AIC%3F↩︎