11  直角双曲线的修正模型

ZiPiao (2010) 直角双曲线修正模型的表达式如式 公式  11.1 所示：

P_{n} = \alpha \frac{1-\beta I}{1+\gamma I} I - R_{d} \tag{11.1}

其中，\beta 和 \gamma 为系数，\beta光抑制项，\gamma光饱和项，单位为 m^{2}\cdot s\cdot\mu mol^{-1}，其他参数与上文相同，因为该式 公式  11.1 存在极值，因此，必然存在饱和光强和最大净光合速率，分别用式 公式  11.2 和式 公式  11.3 求得。

I_{sat} = \frac{\sqrt{\frac{(\beta+\gamma)}{\beta}} - 1}{\gamma} \tag{11.2}

P_{nmax} = \alpha\left(\frac{\sqrt{\beta+\gamma}-\sqrt{\beta}}{\gamma}\right)^{2}-R_{d} \tag{11.3}

该模型的优点为拟合结果中光饱和点和最大净光合速率均接近实测值，还可以拟合饱和光强之后光合速率随光强下降段的曲线。

11.1 直角双曲线修正模型的实现

Code
library(minpack.lm)

# 读取数据，同fitaci数据格式
lrc <- read.csv("data/lrc.csv")
lrc <- subset(lrc, Obs > 0)

# 光响应曲线没有太多参数，
# 直接调出相应的光强和光合速率
# 方便后面调用
lrc_Q <- lrc$PARi
lrc_A <- lrc$Photo 

# 模型的拟合
lrcnls <- nlsLM(lrc_A ~ alpha * ((1 - 
              beta*lrc_Q)/(1 + gamma * lrc_Q)) * lrc_Q - Rd,
                start=list(alpha = 0.07, beta = 0.00005,
                           gamma=0.004, Rd = 0.2)
                )
fitlrc_mrec <- summary(lrcnls)

# 饱和点计算
Isat <-  (sqrt((fitlrc_mrec$coef[2,1] + fitlrc_mrec$coef[3,1])/
              fitlrc_mrec$coef[2,1]) -1)/fitlrc_mrec$coef[3,1]
# 补偿点计算
Ic <- (
  -(fitlrc_mrec$coef[3, 1] * fitlrc_mrec$coef[4, 1] - 
  fitlrc_mrec$coef[1, 1]) - sqrt((fitlrc_mrec$coef[3, 1] * 
  fitlrc_mrec$coef[4, 1] - fitlrc_mrec$coef[1, 1])^2- 
  (4 * fitlrc_mrec$coef[1, 1] * fitlrc_mrec$coef[2, 1] * 
  fitlrc_mrec$coef[4, 1])))/
  (2*fitlrc_mrec$coef[1,1]*fitlrc_mrec$coef[2,1])

## 拟合图形
library(ggplot2)
light <- data.frame(lrc_Q = lrc$PARi, lrc_A = lrc$Photo)

mod_rec_form <-  y ~ 
  alpha * ((1 - beta*x)/(1 + gamma * x)) * x - Rd

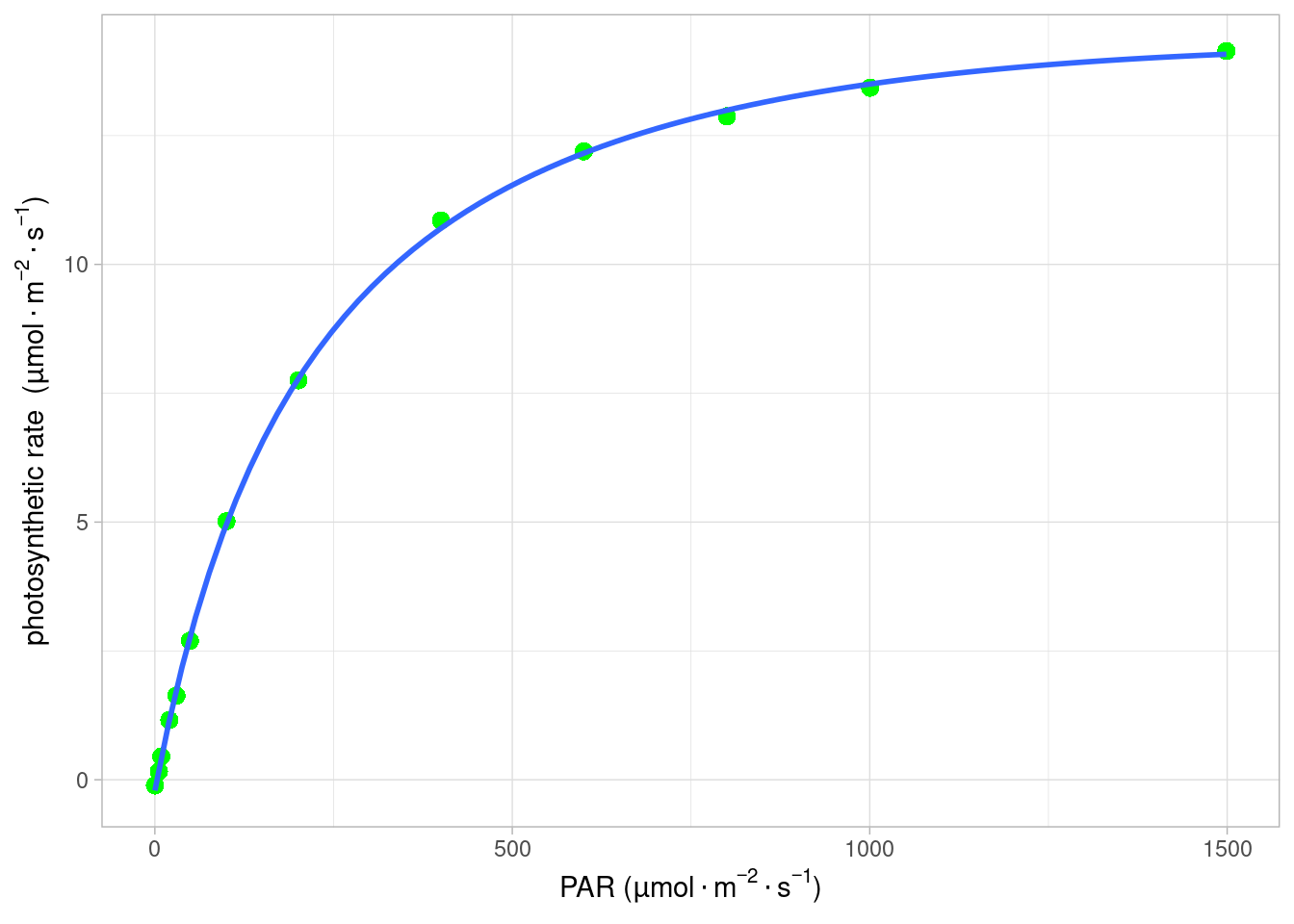
ggplot(light, aes(x = lrc_Q, y = lrc_A)) + 
  geom_point(shape = 16, size = 3, color = "green") + 
  geom_smooth(method="nls", 
    formula = mod_rec_form, 
    se = FALSE, method.args = list(
    start = c(alpha = 0.07, beta = 0.00005,
              gamma=0.004, Rd = 0.2), 
    aes(x =lrc_Q, y = lrc_A, 
    color='blue', size = 1.2))
  )+
  labs(y=expression(paste("photosynthetic rate  ", 
          "(", mu, mol%.%m^-2%.%s^-1, ")")), 
       x=expression(paste("PAR ", 
           "(", mu, mol%.%m^-2%.%s^-1, ")")))+
  theme_light()
Figure 11.1: 直角双曲线修正模型拟合
Table 11.1: 直角双曲线修正模型计算参数
Estimate Std. Error t value Pr(>|t|)
alpha 0.0730858 0.0021209 34.460183 0.0000000
beta 0.0000501 0.0000133 3.776115 0.0043751
gamma 0.0040622 0.0001955 20.773916 0.0000000
Rd 0.2156186 0.0543505 3.967190 0.0032685

尽管修正模型可以方便的计算饱和点和补偿点，但如同 Lobo 等 (2013) 所指出，双曲线模型对其结果的计算常有超出生态学意义范围的值1，因此对模型的选择不能一概而论，需根据实际情况而选择。

  1. 例如本例的数据结果↩︎