15  Aci 曲线拟合相关

ACi 曲线的拟合，有三个软件包来实现，分别是 plantecophys, plantecowraps, photosynthesis （章节 3）。我们分别来看一下他们的实现方式。

15.1 plantecophys 拟合

plantecophys (章节 3) 里拟合二氧化碳的函数本质上只有一个 fitaci，只不过为了一次拟合多个处理的数据，在其基础上将 fitaci 扩展为了 fitacis。

15.1.1 fitaci 函数介绍

fitaci 的用法如下¹：

fitaci(data, varnames = list(ALEAF = "Photo", 
  Tleaf = "Tleaf", Ci = "Ci", PPFD = "PARi", 
  Rd = "Rd"), Tcorrect = TRUE, Patm = 100, 
  citransition = NULL, quiet = FALSE, 
  startValgrid = TRUE, fitmethod = 
  c("default", "bilinear", "onepoint"), 
  algorithm = "default", fitTPU = FALSE, 
  useRd = FALSE, PPFD = NULL, Tleaf = NULL, 
  alpha = 0.24, theta = 0.85, gmeso = NULL, 
  EaV = 82620.87, EdVC = 0, delsC = 645.1013,
  EaJ = 39676.89, EdVJ = 2e+05, 
  delsJ = 641.3615, GammaStar = NULL, 
  Km = NULL, id = NULL, ...)

## S3 method for class 'acifit'
plot(x, what = c("data", "model", "none"),
     xlim = NULL, ylim = NULL, whichA = c(
       "Ac", "Aj", "Amin", "Ap"), add = FALSE,
pch = 19, addzeroline = TRUE, addlegend = 
  !add, legendbty = "o",transitionpoint = TRUE, 
linecols = c("black", "blue", "red"), lwd = c(1,
2), ...)

主要参数注释：

• data：需要分析的数据，必须为 .data.frame。 格式。

• varnames：数据的表头，此处函数默认的表头为 LI-6400 的表头，分析 LI-6400 的数据时可以不用填写，直接使用默认的参数即可²。

• Tcorrect：如果为 TRUE，那么 J_{max}、V_{cmax} 的结果为温度校正结果，若 Tcorrect = FALSE，则为测量温度下的结果。

• Patm：为外界大气压。

• citransition：参见详，若提供该选项，则 J_{max}、V_{cmax} 的区域则分别拟合³。

• fitmethod：参见详解。

• fitTPU：是否拟合 TPU 限制，默认为 FALSE，参见详解。

• x：对于plot.acifit，x 为fitaci返回的对象，简单理解为 将 fitaci 函数拟合结果赋值给一个变量，此处plot函数实际上为plot.acifit。

• what：利用基础做图工具，默认为对数据和模型进行作图。

• whichA：默认为对所有的光合速率进行作图（Aj=Jmax-limited (蓝色), Ac=Vcmax- limited (红色), Hyperbolic minimum (黑色)), TPU-limited rate (Ap, 如果模型有计算结果）。

其余参数请参考 FvCB 模型 Farquhar, Caemmerer, 和 Berry (1980) 及查看 plantecophys 的帮助文档。

fitaci函数详解

• 默认为非线性拟合，详见 Duursma (2015)。

• bilinear 方法使用两次线性拟合方法首先拟合 V_{cmax} 和 R_{d}，然后再拟合J_{max}，过渡点的选择为对所有数据拟合最适的点，类似 Gu 等 (2010) 的方法。该方法的优势时无论如何，都会返回拟合结果，尤其是非线性拟合失败时使用该方法，但若默认方法失败时，需首先检查是否数据存在问题。两种拟合方法的结果有轻微的差别⁴。

• onepoint 参考 De Kauwe 等 (2016)。该方法不同于前面所提到的 ACi 曲线测量，有一系列的前提，但测量比较快。

• citransition 使用时，数据将被区分为 V_{cmax} 限制（Ci < citransition ）区域，以及 J_{max} 限制 (Ci > citransition) 区域。

• fitTPU：如果要计算TPU，要设置 fitTPU = TRUE，并且 fittingmethod = “bilinear”。但需要注意，当 TPU 被计算时，没有 J_{max} 限制的点的存在是可能的。TPU限制的发生是在A值不随 CO_{2} 的增加而增加时发生的，因此计算 TPU 是否有返回值，取决于测量数据是否有此情况出现。

15.1.2 fitaci 的使用

首先安装 plantecophys:

install.packages("plantecophys", dependencies = TRUE)

如果使用 LI-6800，为方便起见，可以使用我修改后的 plantecophys2:

remotes::install_git("https://gitee.com/zhu_jie_dong/plantecophys2")

我们先看一个使用 LI-6400 的例子：

library("plantecophys")

# 利用read.csv读取数据文件，
# 我的路径为当前工作路径的data文件夹内
aci <- read.csv("data/aci.csv")

# 防止可能出现的NA值
aci <- subset(aci, Obs > 0)

# 不修改默认参数对数据进行拟合
acifit <- fitaci(aci)

# 查看拟合结果
summary(acifit)

Result of fitaci.

Data and predictions:
           Ci      Ameas    Amodel         Ac        Aj   Ap        Rd VPD
5    53.47985 -0.6575974 -0.514689 -0.3552037  0.000000 1000 0.1594498 1.5
4    85.82530  1.7971569  1.929261  2.0888576  5.068534 1000 0.1594498 1.5
3   150.67623  6.4525814  6.417603  6.5777532 12.755503 1000 0.1594498 1.5
2   217.32002 10.6562220 10.535462 10.6965881 17.519644 1000 0.1594498 1.5
1   286.39751 14.2848912 14.336589 14.4993989 20.749311 1000 0.1594498 1.5
6   292.56161 15.4296572 14.974916 15.1383711 20.852617 1000 0.1594498 1.5
7   292.96456 15.7134791 15.056480 15.2200531 20.831099 1000 0.1594498 1.5
8   450.64285 22.2659015 23.011519 23.1976010 25.186940 3000 0.1594498 1.5
9   622.03873 26.5135040 27.648500 30.4281411 27.837462 3000 0.1594498 1.5
10  992.08737 30.3898585 30.630046 42.3998197 30.797661 3000 0.1594498 1.5
11 1558.96968 33.6267056 32.663802 54.9948295 32.828111 3000 0.1594498 1.5
12 1756.16396 33.3152783 33.098149 58.5844541 33.261966 3000 0.1594498 1.5
      Tleaf         Cc     PPFD Patm Ci_original
5  31.12332   53.47934 1800.490  100    53.47985
4  30.99093   85.82723 1800.558  100    85.82530
3  30.82872  150.68265 1800.140  100   150.67623
2  30.63983  217.33057 1800.524  100   217.32002
1  30.46890  286.41186 1800.701  100   286.39751
6  31.26338  292.57660 1799.923  100   292.56161
7  31.41866  292.97963 1799.975  100   292.96456
8  31.54122  450.66588 1799.826  100   450.64285
9  31.63493  622.06640 1799.578  100   622.03873
10 31.73910  992.11803 1800.055  100   992.08737
11 31.86938 1559.00238 1800.022  100  1558.96968
12 31.96654 1756.19709 1799.585  100  1756.16396

Root mean squared error:  1.889701 

Estimated parameters:
         Estimate Std. Error
Vcmax  49.2616183  1.5152403
Jmax  126.6205411  2.2816264
Rd      0.1594498  0.4001301
Note: Vcmax, Jmax are at 25C, Rd is at measurement T.

Curve was fit using method:  default 

Parameter settings:
Patm = 100
 alpha = 0.24
 theta = 0.85
 EaV = 82620.87
 EdVC = 0
 delsC = 645.1013
 EaJ = 39676.89
 EdVJ = 2e+05
 delsJ = 641.3615

Estimated from Tleaf (shown at mean Tleaf):
GammaStar =  58.61138 
Km =  1223.279 

acifit_linear <- fitaci(aci,  fitmethod = "bilinear", quiet = TRUE)
summary(acifit_linear)

Result of fitaci.

Data and predictions:
           Ci      Ameas     Amodel         Ac        Aj   Ap        Rd VPD
5    53.47985 -0.6575974 -0.7389447 -0.3560483  0.000000 1000 0.3828608 1.5
4    85.82530  1.7971569  1.7108198  2.0938246  5.138366 1000 0.3828608 1.5
3   150.67623  6.4525814  6.2098476  6.5933940 12.931333 1000 0.3828608 1.5
2   217.32002 10.6562220 10.3375299 10.7220229 17.761317 1000 0.3828608 1.5
1   286.39751 14.2848912 14.1477696 14.5338762 21.035722 1000 0.3828608 1.5
6   292.56161 15.4296572 14.7876514 15.1743678 21.139657 1000 0.3828608 1.5
7   292.96456 15.7134791 14.8694171 15.2562440 21.117718 1000 0.3828608 1.5
8   450.64285 22.2659015 22.8464806 23.2527613 25.533374 3000 0.3828608 1.5
9   622.03873 26.5135040 27.8030690 30.5004944 28.220254 3000 0.3828608 1.5
10  992.08737 30.3898585 30.8295808 42.5006398 31.221072 3000 0.3828608 1.5
11 1558.96968 33.6267056 32.8913778 55.1255986 33.279305 3000 0.3828608 1.5
12 1756.16396 33.3152783 33.3316070 58.7237587 33.719013 3000 0.3828608 1.5
      Tleaf         Cc     PPFD Patm Ci_original
5  31.12332   53.47911 1800.490  100    53.47985
4  30.99093   85.82701 1800.558  100    85.82530
3  30.82872  150.68244 1800.140  100   150.67623
2  30.63983  217.33037 1800.524  100   217.32002
1  30.46890  286.41167 1800.701  100   286.39751
6  31.26338  292.57641 1799.923  100   292.56161
7  31.41866  292.97944 1799.975  100   292.96456
8  31.54122  450.66572 1799.826  100   450.64285
9  31.63493  622.06656 1799.578  100   622.03873
10 31.73910  992.11823 1800.055  100   992.08737
11 31.86938 1559.00260 1800.022  100  1558.96968
12 31.96654 1756.19733 1799.585  100  1756.16396

Root mean squared error:  2.013045 

Estimated parameters:
         Estimate Std. Error
Vcmax  49.3787547  3.4815555
Jmax  128.5546403         NA
Rd      0.3828608  0.4697008
Note: Vcmax, Jmax are at 25C, Rd is at measurement T.

Curve was fit using method:  bilinear 

Parameter settings:
Patm = 100
 alpha = 0.24
 theta = 0.85
 EaV = 82620.87
 EdVC = 0
 delsC = 645.1013
 EaJ = 39676.89
 EdVJ = 2e+05
 delsJ = 641.3615

Estimated from Tleaf (shown at mean Tleaf):
GammaStar =  58.61138 
Km =  1223.279 

# 仅查看拟合参数, 比较两种拟合参数的差异
coef(acifit_linear)

      Vcmax        Jmax          Rd 
 49.3787547 128.5546403   0.3828608 

coef(acifit)

      Vcmax        Jmax          Rd 
 49.2616183 126.6205411   0.1594498 

需要注意，plantecophys 的 Rd 不需要带负号，即上面的仅仅表示呼吸速率的值。

# 设置作图参数，图形的边距及分为1行两列输出图形
op <- par(no.readonly = TRUE)
par(mar = c(4.5, 4.5, 2, 2))
par(mfrow = c(1, 2))
# 对两种拟合参数的结果作图，查看模型拟合是否正常
plot(acifit, addlegend = FALSE)
legend(x = 500, y = 10, 
       legend = c(expression(paste(A[c])), 
                expression(paste(A[j])),
                "Limiting rate"),
       lty = c(1, 1, 1),
       col =c("red", "blue", "black") 
         )
mtext(" fitmethod = 'default' ")

plot(acifit_linear, addlegend = FALSE)
legend(x = 500, y = 10, 
       legend = c(expression(paste(A[c])), 
                  expression(paste(A[j])),
                  "Limiting rate"),
       lty = c(1, 1, 1),
       col =c("red", "blue", "black") 
)
mtext("fitmethod = 'bilinear' ")
par <- op

Figure 15.1: fitmethod 为非线性和线性拟合的差异

如果需要导出数据做他用，使用 Rstudio 的话，其自动补全的功能在选择数据上更方便 (即输入拟合的名称 + $ 符号后，自动补全会弹出提示)。例如导出预测值和系数分别使用如下方式：

# 将模型拟合结果中df（即计算数据）赋给predictaci，
# 并用write.csv导出
predictaci <- acifit$df
write.csv(acifit$df, file = "acipredict.csv")
write.csv(coef(acifit), file = "coefaci.csv")

需要注意的是，因为非线性拟合需要一个初值，因此，使用默认方式（非线性拟合）的时候，会存在可能的拟合失败现象，此时可以使用 fitmethod = "bilinear"，二者结果略有差别。

一次拟合多条 ACi 曲线

fitacis 函数实际上是 fitaci 函数的扩展，方便一次拟合多条曲线⁵。函数的参数如下：

fitacis(data, group, fitmethod = c("default", 
        "bilinear"),progressbar = TRUE, 
        quiet = FALSE, id = NULL, ...)

## S3 method for class 'acifits'
plot(x, how = c("manyplots", "oneplot"), 
     highlight = NULL, ylim = NULL, 
     xlim = NULL, add = FALSE, what = c("model",
     "data", "none"), ...)

主要参数详解：

实际上 fitacis 与 fitaci 模型算法完全一致，只不过增加了一个 group 参数，用于区分不同测量的数据，具体请参考举例内容。

fitacis 函数应用举例

下文代码根据 plantecophys 中的示例代码修改，进行演示，原代码请参考其帮助文档。

library(plantecophys)
# 只提取前10个不同测量的数据，节省时间进行举例
manyacidat2 <- droplevels(manyacidat[manyacidat$Curve %in% 
                                       levels(manyacidat$Curve)[1:10],])

# 对多条曲线进行拟合，使用bilinear方法，
# 仅仅因为其比非线性拟合节省时间
fits <- fitacis(manyacidat2, group = "Curve", fitmethod="bilinear", quiet = TRUE)

# 拟合结果为list，我们可以只提取第一个的拟合结果
fits[[1]]

Result of fitaci.

Data and predictions:
           Ci      Ameas     Amodel         Ac        Aj   Ap        Rd VPD
2    53.23129 -0.4401082  0.1014381  0.9601119  2.548123 1000 0.8586158 1.5
3    79.47367  2.4824630  2.1937702  3.0526198  7.036734 1000 0.8586158 1.5
4   116.74688  5.4531712  4.9419337  5.8011511 11.392394 1000 0.8586158 1.5
5   188.00801  9.7099879  9.5705964 10.4310194 16.447715 1000 0.8586158 1.5
6   278.44662 14.8225766 14.4261545 15.2897486 19.977583 1000 0.8586158 1.5
7   343.03259 17.7982155 17.4602014 18.3289218 21.639847 1000 0.8586158 1.5
1   344.72152 17.9244012 17.3165146 18.1849643 21.534276 1000 0.8586158 1.5
14  344.74839 16.7933747 17.6853306 18.5545917 21.774261 1000 0.8586158 1.5
8   588.08078 23.8925326 24.1309683 27.0327638 25.020148 3000 0.8586158 1.5
9   833.25547 26.5674409 25.7783026 33.0856065 26.647921 3000 0.8586158 1.5
10 1136.99222 25.9787890 26.8108335 38.1296944 27.676768 3000 0.8586158 1.5
11 1436.86370 26.6110657 27.5409345 42.0628463 28.405453 3000 0.8586158 1.5
12 1536.46772 27.4018784 27.7965881 43.3773689 28.660781 3000 0.8586158 1.5
13 1731.76400 28.6752069 28.0952804 45.2475932 28.959041 3000 0.8586158 1.5
      Tleaf         Cc     PPFD Patm Ci_original
2  24.55873   53.23139 1799.959  100    53.23129
3  24.58292   79.47586 1799.590  100    79.47367
4  24.71278  116.75183 1799.819  100   116.74688
5  24.73687  188.01759 1800.371  100   188.00801
6  24.67508  278.46106 1800.233  100   278.44662
7  24.76596  343.05006 1799.575  100   343.03259
1  24.51593  344.73886 1800.356  100   344.72152
14 24.94098  344.76609 1799.964  100   344.74839
8  24.83785  588.10494 1799.477  100   588.08078
9  24.91185  833.28127 1799.969  100   833.25547
10 24.87314 1137.01906 1799.525  100  1136.99222
11 24.95914 1436.89126 1799.615  100  1436.86370
12 25.04542 1536.49554 1799.784  100  1536.46772
13 25.07566 1731.79212 1799.160  100  1731.76400

Root mean squared error:  2.196037 

Estimated parameters:
         Estimate Std. Error
Vcmax  65.0009909  1.3720635
Jmax  131.7980133         NA
Rd      0.8586158  0.2876248
Note: Vcmax, Jmax are at 25C, Rd is at measurement T.

Curve was fit using method:  bilinear 

Parameter settings:
Patm = 100
 alpha = 0.24
 theta = 0.85
 EaV = 82620.87
 EdVC = 0
 delsC = 645.1013
 EaJ = 39676.89
 EdVJ = 2e+05
 delsJ = 641.3615

Estimated from Tleaf (shown at mean Tleaf):
GammaStar =  42.31453 
Km =  698.2084 

# 使用sapply提取拟合结果的RMSE(均方根误差)
rmses <- sapply(fits, "[[", "RMSE")
plot(rmses, type='h', ylab="RMSE", xlab="Curve nr")
# 对最差的拟合结果进行作图
plot(fits[[which.max(rmses)]])

Figure 15.2: fitacis作图结果

Figure 15.3: fitacis作图结果

可以看出，fitaci 和 fitacis 用法基本一致，各行代码均已经注释，更详细用法请参函数考帮助。

15.1.3 fitmethod = “onepoint” 介绍

De Kauwe 等 (2016) 发表了关于 one point 方法计算 V_{cmax} 和 J_{max} 的文章，在 2017 年 11 月的更新中，plantecophys 将对应的 python 代码移植到了 plantecophys， 该方法并非使用一个点计算 V_{cmax} 和 J_{max}，而是对数据集中的每一个点的值进行估计，使用的方法为逆向了光合作用方程。输出则是将原始数据中加入了 V_{cmax} 和 J_{max} 的计算结果，当然一如既往的可以使用温度校准的方法。为提升测量的准确性，最佳方案是有测量的 Rd 值。也就是 useRd 被默认启用。它的假设是在外部环境 CO₂ 浓度和饱和光下。

基于上面的描述，他们的模型如下：

\hat{V}_{cmax} = (A_{sat} + R_{day}) \frac{C_i + K_m}{C_i - \Gamma^*} \tag{15.1}

其中：K_m 为米氏常数，其计算为：

K_m = K_c (1 + \frac{O_i}{K_o}) \tag{15.2}

未知参数均由文献中的方法进行计算，具体可参考 De Kauwe 等 (2016) 的原文,但上述方法的缺陷是还需要 R_day，因此作者使用了1.5% V_cmax 作为 R_day，因此公式 公式  15.1 可变换为：

\hat{V}_{cmax} = A_{sat} (\frac{C_i + K_m}{C_i - \Gamma^*} - 0.015) \tag{15.3}

另一个重要的模型的假设为 J_max 与 V_cmax 是成比例的， J_max 的计算是通过 C_i transition point 来实现的，文章中的比值均值为 1.9，范围在 1.68 ~ 2.14 之间。

15.1.4 使用 ‘onepoint’ 单独计算 V_cmax 和 J_max

目前我手头没有相应数据，仅有使用 LI-6400 测试 auto log 2 时的一个数据，我们用这个来示范该方法的使用：

one_data <- read.csv("data/onepoint.csv")

Table 15.1: onepoint 使用的数据

Obs	HHMMSS	FTime	EBal.	Photo	Cond	Ci	Trmmol	VpdL	CTleaf	Area	BLC_1	StmRat	BLCond	Tair	Tleaf	TBlk	CO2R	CO2S	H2OR	H2OS	RH_R	RH_S	Flow	PARi	PARo	Press	CsMch	HsMch	CsMchSD	HsMchSD	CrMchSD	HrMchSD	StableF	BLCslope	BLCoffst	f_parin	f_parout	alphaK	Status	fda	Trans	Tair_K	Twall_K	R.W.m2.	Tl.Ta	SVTleaf	h2o_i	h20diff	CTair	SVTair	CndTotal	vp_kPa	VpdA	CndCO2	Ci_Pa	Ci.Ca	RHsfc	C2sfc	AHs.Cs
1	14:12:43	347.0	0	10.519216	0.1369336	263.0905	1.963046	1.445782	25.89411	6	1.42	1	2.84	25.86572	25.89411	25.86697	412.5374	398.9832	16.98853	19.29724	50.16200	56.97891	500.3231	1198.761	7.497697	98.84273	2.011996	-0.3824501	0.1618589	0.0039255	0.1864786	0.0030409	1.0000000	-0.2195652	2.737392	1	0	0.16	111115	0.8338718	0.0019630	299.0441	299.0157	191.8018	1.191025	3.353173	33.92433	14.62709	25.87991	3.350355	0.1306349	1.907392	1.442964	0.0821903	26.00458	0.6594024	57.74196	393.9829	0.0154169
2	14:13:04	369.0	0	10.361122	0.1357092	264.1135	1.946022	1.445559	25.89542	6	1.42	1	2.84	25.86854	25.89542	25.86977	412.5459	399.1890	17.01363	19.30231	50.22723	56.98380	500.3223	1198.748	7.486364	98.84175	2.018435	-0.3787848	0.2174792	0.0025482	0.2455426	0.0025012	1.0000000	-0.2195652	2.737392	1	0	0.16	111115	0.8338705	0.0019460	299.0454	299.0185	191.7997	1.199722	3.353433	33.92729	14.62498	25.88198	3.350765	0.1295200	1.907874	1.442891	0.0814842	26.10544	0.6616252	57.73418	394.2638	0.0151724
3	14:13:25	373.0	0	10.207166	0.1342114	264.8348	1.925734	1.445717	25.89660	6	1.42	1	2.84	25.87186	25.89660	25.87317	412.5393	399.3762	17.03833	19.30316	50.29006	56.97489	500.3188	1198.737	7.489428	98.84142	2.018435	-0.3787848	0.2174792	0.0025482	0.2455426	0.0025012	1.0000000	-0.2195652	2.737392	1	0	0.16	111115	0.8338647	0.0019257	299.0466	299.0219	191.7980	1.210137	3.353668	33.92979	14.62663	25.88423	3.351212	0.1281551	1.907951	1.443261	0.0806199	26.17665	0.6631213	57.71117	394.5242	0.0149311
4	14:13:41	389.5	0	9.547416	0.1281947	269.6337	1.854272	1.454248	25.94020	6	1.42	1	2.84	25.91845	25.94020	25.92104	413.8090	401.4666	17.12559	19.30638	50.40359	56.82203	500.3162	1199.245	7.449210	98.83208	2.018435	-0.3787848	0.2174792	0.0025482	0.2455426	0.0025012	1.0000000	-0.2195652	2.737392	1	0	0.16	111115	0.8338604	0.0018543	299.0902	299.0684	191.8792	1.247158	3.362337	34.02071	14.71433	25.92933	3.360173	0.1226580	1.908089	1.452084	0.0771402	26.64846	0.6716216	57.48324	396.9282	0.0138266
5	14:16:16	540.0	0	10.288968	0.1376602	267.9198	2.009217	1.471788	26.01813	6	1.42	1	2.84	26.01478	26.01813	26.02164	413.9044	400.5999	16.92567	19.28878	49.53554	56.44850	500.3043	1200.785	7.497018	98.81870	2.018435	-0.3787848	0.2174792	0.0025482	0.2455426	0.0025012	0.6666667	-0.2195652	2.737392	1	0	0.16	111115	0.8338405	0.0020092	299.1681	299.1648	192.1257	1.174669	3.377880	34.18260	14.89382	26.01646	3.377546	0.1312960	1.906093	1.471453	0.0826090	26.47549	0.6687965	57.30143	395.7090	0.0148991
6	14:16:32	555.5	0	10.178603	0.1381995	269.5898	2.016100	1.471138	26.01657	6	1.42	1	2.84	26.02212	26.01657	26.02939	413.6639	400.4885	16.92345	19.29468	49.49181	56.42595	500.2979	1200.879	7.569045	98.80596	2.018435	-0.3787848	0.2174792	0.0025482	0.2455426	0.0025012	0.6666667	-0.2195652	2.737392	1	0	0.16	111115	0.8338298	0.0020161	299.1666	299.1721	192.1406	1.172561	3.377567	34.18384	14.88916	26.01934	3.378122	0.1317865	1.906429	1.471693	0.0829197	26.63708	0.6731525	57.32389	395.6501	0.0147473

Table 15.1 数据为同一个叶片连续记录数据，故所有的光合速率十分接近。

使用方法：

library(plantecophys)

one_data <- subset(one_data, Obs > 0)
one_data$Rd <- 0.5
aci_fit <- fitaci(one_data, fitmethod = "onepoint")

Table 15.2: onepoint 法计算的结果

aci_fit.Photo	aci_fit.Vcmax	aci_fit.Jmax
10.519216	47.06893	71.73759
10.361122	46.22091	70.51059
10.207166	45.44617	69.35838
9.547416	41.86217	64.24400
10.288968	45.09335	69.36954
10.178603	44.37360	68.41628
10.348184	45.61262	69.98563
10.088908	43.96870	67.78267
10.382970	45.83416	70.28272
10.314660	45.32629	69.64235
10.249137	44.86035	69.04578
10.263942	45.03290	69.23316
10.276372	45.06777	69.30476
10.310315	45.41163	69.69375
10.257607	45.10509	69.26665
10.268318	45.10636	69.30563
10.249136	45.08506	69.22086
10.286432	45.23213	69.46825
10.304019	45.40981	69.66987
10.232778	44.93236	69.04323
10.211444	44.87301	68.92133
10.261779	45.27150	69.41197
10.372243	45.88799	70.28733
9.865629	42.90010	66.16012
10.494170	46.74011	71.39036
10.218001	45.02652	69.06497
10.059445	44.09354	67.77443
10.428858	46.47593	70.95132
10.250793	45.30113	69.39661
9.912939	43.36453	66.68832
10.199344	45.25700	69.18076
10.391926	46.39390	70.75653
10.160686	44.88657	68.75316
10.024682	44.18376	67.72287
10.129775	44.92784	68.67708
10.141083	45.00936	68.78099
10.001353	44.25706	67.69872
10.292306	45.99487	70.09022
10.107537	44.81090	68.50677
10.045704	44.52225	68.06286
10.020921	44.45621	67.92429
10.110870	45.11312	68.75747
10.002926	44.42129	67.83392
10.084427	45.05038	68.61609
9.997523	44.53516	67.90526
10.031004	44.79683	68.22931
10.067866	45.01510	68.53037
9.913409	44.05520	67.23265
10.021746	44.87409	68.25803
9.913314	44.20530	67.35073
9.993697	44.80203	68.10315
9.851695	44.01827	66.98918
9.736275	43.13847	65.89470
9.797319	43.98036	66.76973
9.626554	42.91998	65.34117
9.471773	41.68336	63.83331
9.646700	42.87917	65.37916
9.644842	42.99673	65.46524
9.758413	43.70607	66.41972
9.553852	42.50445	64.76295
9.662671	43.28157	65.75264
9.563656	42.70328	64.95411
9.672595	43.52788	65.98331
9.548987	42.64583	64.85665
9.597028	43.06762	65.35629
9.564234	42.91240	65.11967
9.528271	42.77665	64.88887
9.516492	42.83815	64.89806
9.473123	42.62617	64.58091
9.448475	42.51675	64.41002
9.456234	42.55351	64.46375
9.480095	42.94755	64.86062
9.363030	42.21889	63.88107
9.311755	41.93995	63.48342
9.459983	43.05099	64.87112
9.483853	43.30531	65.15723
9.027537	40.30433	61.22108
9.476729	43.44072	65.23563
9.280183	42.12853	63.52291
9.261344	42.17840	63.49744
9.334307	42.85683	64.28533
9.051123	41.06857	61.90318
9.270810	42.51712	63.79523
9.330762	43.01265	64.39291
9.218163	42.26923	63.41804
9.085934	41.60645	62.44411
9.083060	41.74496	62.54482
9.132510	42.02581	62.93301
9.131158	42.10676	62.99170
9.145548	42.35821	63.24067
9.059605	41.85986	62.55140
9.091451	42.25809	62.97554
9.070366	42.19632	62.85631
8.943521	41.35936	61.76031
8.975535	41.65581	62.10145
8.973756	41.81212	62.22232
8.962861	41.76093	62.14239
8.904978	41.49087	61.73147
8.918707	41.60684	61.86895
8.968677	42.07851	62.41156
8.759890	40.74396	60.64875
8.821386	41.29744	61.29504
8.896446	41.92053	62.04190
8.847126	41.57371	61.60003
8.841565	41.74028	61.71268
8.832967	41.80729	61.73844
8.847937	41.85192	61.82163
8.728196	40.98872	60.72970
8.789579	41.72098	61.52023
8.720803	41.30092	60.95505
8.793964	41.82089	61.60873
8.740789	41.45169	61.13431
8.912781	42.54266	62.58591
8.641433	41.15567	60.56410
8.716064	41.68926	61.24072
8.826706	42.15912	61.99019
8.835380	42.38866	62.20246
8.795586	42.17302	61.89721
8.791231	42.11367	61.83223

需要注意，为保证结果的精确，如果不设定 Rd, 也即文献中的 Rday， 模型是无法计算的，因此 Table 15.2 的示例中虚构了一个。

15.1.5 findCiTransition 函数

对于计算不同 ACi 限制阶段过渡点的方式，可以使用 CiTransition 的函数，第一点为 Ac ~ Aj，第二点为 Aj ~ Ap，并且仅在计算 TPU 的前提下才会有第二点出现。

findCiTransition(object, ...)

参数使用，object 为 fitaci 函数对象，或者整个的 Photosyn 函数。 … 为使用 Photosyn 时可传递的参数。默认的 fitaci 对象作图会标记该点，如图 Figure 15.1。 数据的计算也非常简单：

findCiTransition(acifit)

   Ac_Aj    Aj_Ap 
538.0701       NA 

15.2 photosynthesis 拟合

相比plantecophys， photosynthesis (章节 3) 做了一些改进，但基本使用非常相似。我们使用和 plantecophys 相同的数据集进行演示。

这里官方文档说是温度使用的摄氏度，但是 vignette 使用的是 K，经过验证，应该是 K 才能拟合。。

library(photosynthesis)

aci$TLEAF <- aci$Tleaf + 273.15
fit <-
  fit_aci_response(aci,
                   varnames = list(
                     A_net = "Photo",
                     T_leaf = "TLEAF",
                     C_i = "Ci",
                     PPFD = "PARi"
                   ))

我们先观察拟合结果：

reshape2::melt(fit[[1]])

::: {.cell tbl-cap=’ ’} ::: {.cell-output-display}

Table 15.3: 使用 photosynthesis 来拟合 ACi 曲线的结果

variable	value
Num	0.0000000
V_cmax	98.7962878
V_cmax_se	2.1338711
J_max	157.4297453
J	146.2105728
J_se	0.5587627
V_TPU	1000.0000000
V_TPU_se	NA
R_d	-0.1030324
R_d_se	0.2816426
cost	1.9502380
citransition1	536.3407882
citransition2	1757.1639630
V_cmax_pts	8.0000000
J_max_pts	4.0000000
V_TPU_pts	0.0000000
alpha	0.2400000
alpha_g	0.0000000
gamma_star25	42.7500000
Ea_gamma_star	37830.0000000
K_M25	718.4000000
Ea_K_M	65508.2800000
g_mc25	0.0870100
Ea_g_mc	0.0000000
Oconc	21.0000000
theta_J	0.8500000

::: :::

上面使用 melt 纯粹是因为横排数据太长，并非必须。其实也能看出来它拟合 ACi 和非直角双曲线光响应模型是一样的展示结果的方式，图形查看为：

fit[[2]]

使用 photosynthesis 来拟合 ACi 曲线的图形查看

此外，它也有 fit_many 函数用于多组数据的拟合，这个没太大变化，主要是注意分组参数 group，以及使用函数的参数 funct 为 fit_aci_response，此处不再展开介绍。

关于 LI-6800 数据分析示例

为减少单个单元的代码量，同时也为了方便，将 LI-6800 数据分析代码演示放在了 RACiR 单元内演示。

De Kauwe, Martin G, Yan Shih Lin, Ian J Wright, Belinda E Medlyn, Kristine Y Crous, David S Ellsworth, Vincent Maire, I Colin Prentice, Owen K Atkin, 和 Alistair Rogers. 2016. 《A test of the one point method for estimating maximum carboxlation capacity from field measured, light saturated photosynthesis》. New Phytologist 210 (3): 1130.

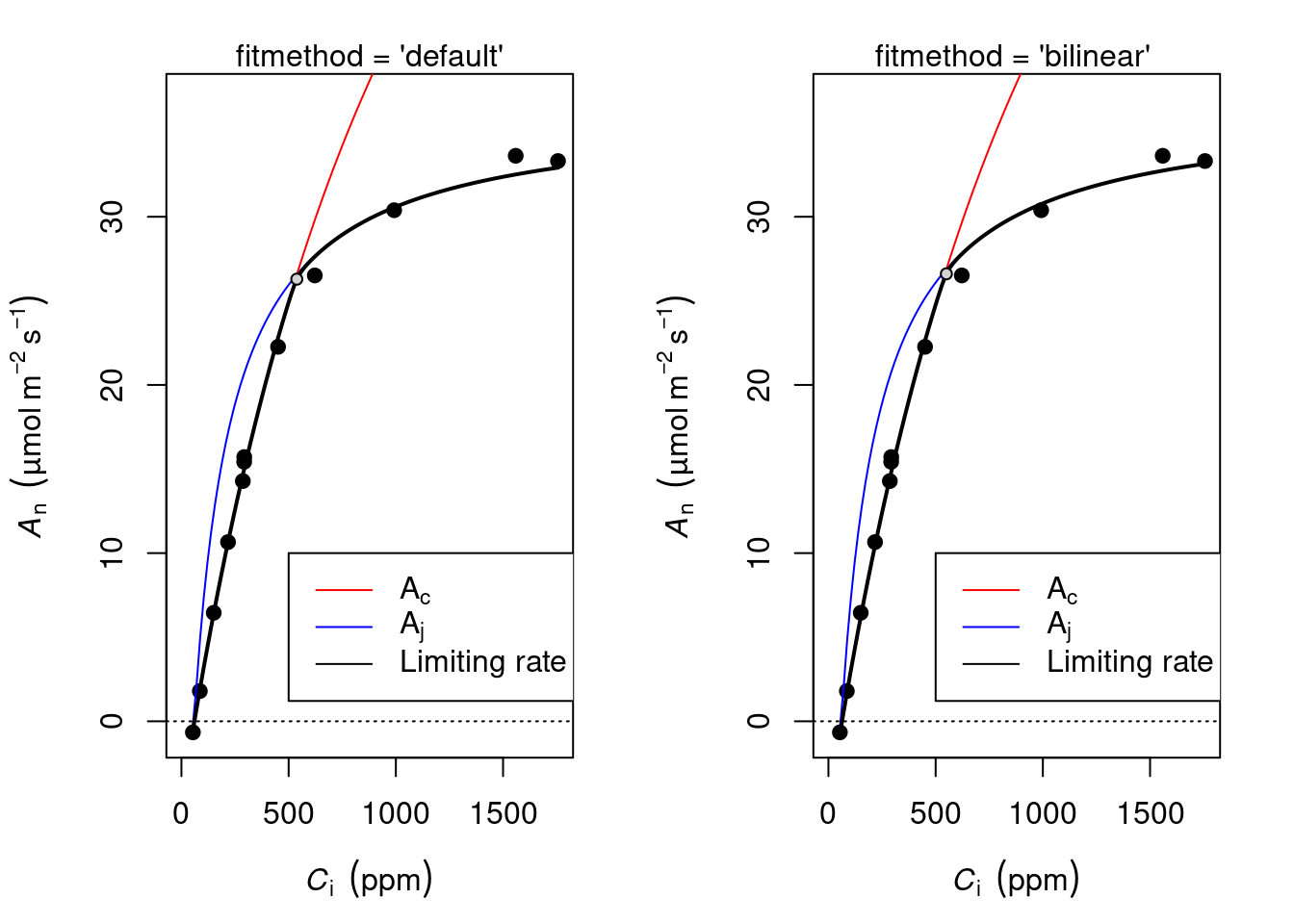
Duursma, Remko A. 2015. 《Plantecophys-An R Package for Analysing and Modelling Leaf Gas Exchange Data》. Plos One 10 (11): e0143346.

Farquhar, G. D., S. Von Caemmerer, 和 J. A. Berry. 1980. 《A biochemical model of photosynthetic CO_2 assimilation in leaves of C3 species.》 Planta 149 (1): 78–90.

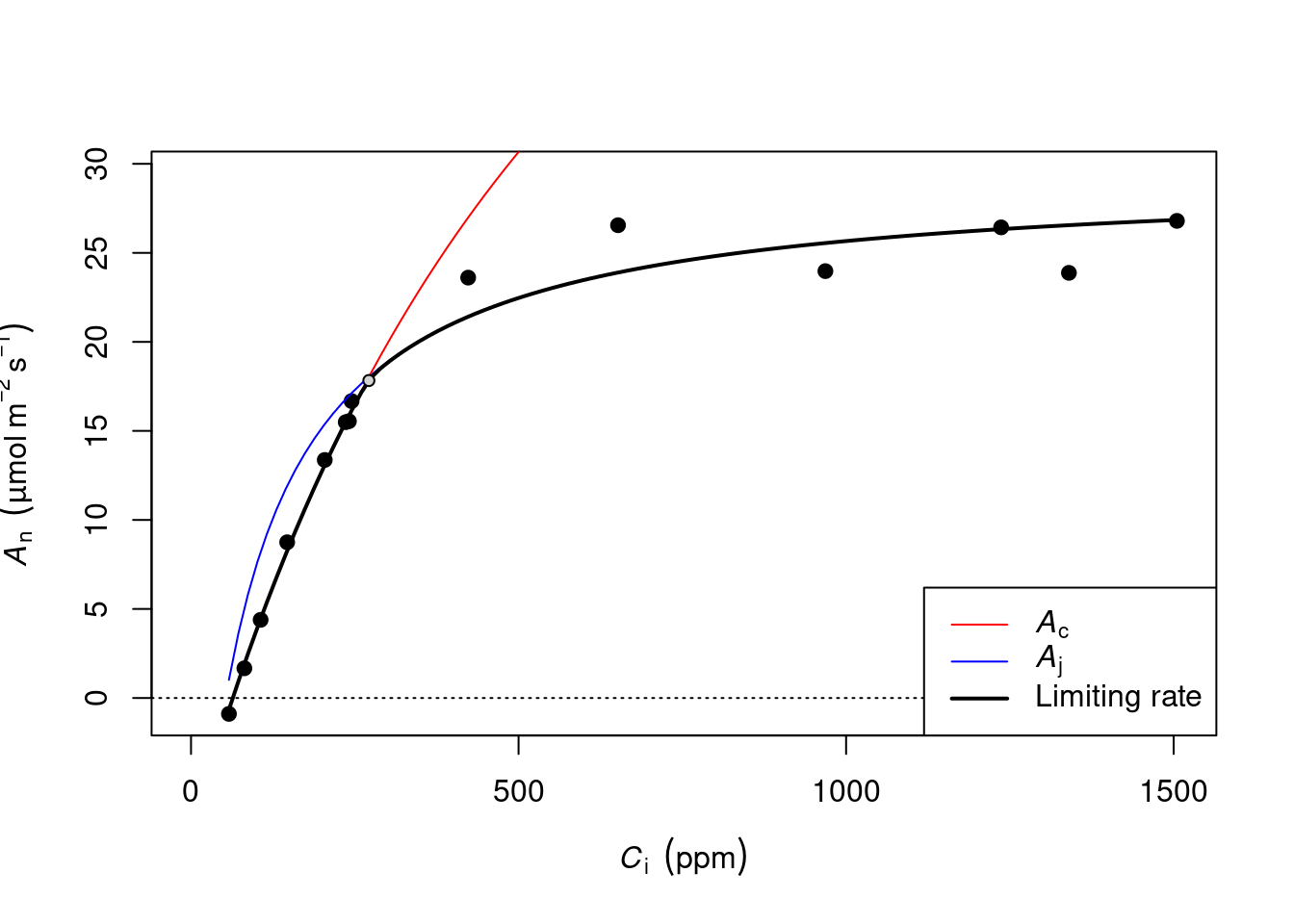
Gu, Lianhong, Stephen G Pallardy, Kevin Tu, Beverly E Law, 和 Stan D Wullschleger. 2010. 《Reliable estimation of biochemical parameters from C-3 leaf photosynthesis-intercellular carbon dioxide response curves》. Plant Cell & Environment 33 (11): 1852–74.

---

1. 仅针对 C3 植物

2. 在 R 中，使用参数的值为默认值时可以不用填写该参数，例如使用默认选项分析 LI-6400 数据时，可只填写 data 项，具体参考 R 的相关入门手册

3. 为Rubisco和RuBP限制的Ci转换点，物种间差异较大，可以通过预实验确定

4. 若默认拟合方法失败，数据也无问题，那么是非线性拟合初始值设定的原因

5. 需要注意，此时fitmethod一般推荐使用bilinear。