第 9 章关于非线性拟合的初始值

在解释初始值之前我们首先需要了解一个数学上的概念——迭代，

“迭代法”也称“辗转法”是一种不断用变量的旧值递推新值的过程。

用通俗但不是特别严谨的说法可解释为：每次执行这种算法时，程序都会从原值（也就是我抄的上面迭代法定义的旧值）推出一个新值。

之所以先介绍这个迭代，原因很简单，非线性拟合就是通过迭代的方法，需要对每一个变量最初的估计值进行不断的迭代，得到一个向一个点收缩或汇聚的值，这个估计值必须在实际值的一定范围内，程序通过不断调整这个值来改善拟合结果。这就解释了上面的问题，初始值是让程序开始运行的前提，不然没法迭代，必须设定。我下面的内容将以 LI-6800 的光响应曲线的测试数据，使用非直角双曲线模型进行拟合来讲解具体的 R 中的一些实现方法，我们首先导入数据，然后再利用这些数据逐个举例不同的确定初始值的方式。

nls <- read.csv("data/nlstest.csv")


# 光响应曲线比较简单，我们将需要的数据直接提取，方便后面操作
lrc_Q <- nls$Qin
lrc_A <- nls$A

9.1 nlsLM 解决方案

nlsLM 来自于 Elzhov et al. (2016) 的 minpack.lm，利用 C 语言的 MINPACK 库，修改了 Levenberg-Marquardt 算法，在实际操作中，很多时候并不准确的输入初始值，他也能得出比较好的拟合结果。但结果未必完美，出现下面让人烦恼的报错：

singular gradient matrix at initial parameter estimates

的概率会大大降低，而且尽管结果不如意，我们也可以利用他的结果缩小初始值的范围，继续尝试其他初始值。

例如下面的例子中，非直角双曲线的 Rd 的初始值我们可以利用暗呼吸的实测值大致估计，同理最大光合速率也是如此，剩下的分别为非直角双曲线曲率，我们暂定为 1，alpha 也暂定为 0.1，使用 nlsLM 进行拟合，结果如下：

library(minpack.lm)

lrcnls_lm <- nlsLM(lrc_A ~ (1/(2*theta))*
        (alpha*lrc_Q+Am-sqrt((alpha*lrc_Q+Am)^2 - 
        4*alpha*theta*Am*lrc_Q))- 
        Rd, start=list(Am=(max(lrc_A)-min(lrc_A)),
        alpha=0.1,Rd=-min(lrc_A),theta=0.8))

结果没有报错，看上去没有问题，那我们观察一下具体的拟合结果：

summary(lrcnls_lm)

## 
## Formula: lrc_A ~ (1/(2 * theta)) * (alpha * lrc_Q + Am - sqrt((alpha * 
##     lrc_Q + Am)^2 - 4 * alpha * theta * Am * lrc_Q)) - Rd
## 
## Parameters:
##        Estimate Std. Error t value Pr(>|t|)    
## Am    12.307570   0.406739  30.259 2.30e-10 ***
## alpha  0.045706   0.003423  13.352 3.09e-07 ***
## Rd     0.656638   0.132646   4.950 0.000791 ***
## theta  0.707522   0.079738   8.873 9.59e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1852 on 9 degrees of freedom
## 
## Number of iterations to convergence: 8 
## Achieved convergence tolerance: 1.49e-08

结果看上去还可以¹⁴。

9.2 作图比对法

模型很多参数可以用已有数据去估计，我们可以只来分析难以判断的参数，流程如下：

Rd、Am等我们可以利用测量值来确定一个范围。
剩余的参数，我们也可以根据经验或文献来有一个大致的判断。
然后我们根据数学的方式来判断哪个参数对曲线形状影响最大（例如在分母上的参数，或者是乘以该参数，该参数可以显著改变计算结果，例如整体乘以或除以 0.1 还是 0.01，像 Rd 之类的参数本身就很小，多数公式中都是减去该值，对结果影响很小，我们通常直接使用实测值）。
将该参数取一系列值带入模型来求解净光合速率。
将计算的A值与光强进行作图，看我们计算的曲线与测量数据点的重合程度，必要时在修改其他参数，使曲线和散点重合度最好，重合程度最高的参数值即为我们需要的初始值。

9.2.1 实现过程

# 我们选择的模型，将其写为一个函数，用于计算净光合速率
expfct <- function(x, Am, alpha, Rd, theta) {
  (1/(2 * theta)) * (alpha * x + Am - 
  sqrt((alpha * x + Am)^2 - 4 * alpha * theta * Am * x)) - Rd
}

# 我们的数据
test <- data.frame(x = lrc_Q, y = lrc_A)

# 先做实测数据的散点图
plot(y ~ x, data = test)

# 利用上面的函数，假定 alpha 的值为0.8，看计算值与测量值重合程度
curve(expfct(x, Am = (max(lrc_A)-min(lrc_A)),
     alpha=0.8, Rd=-min(lrc_A), theta=0.8), add = TRUE
             )

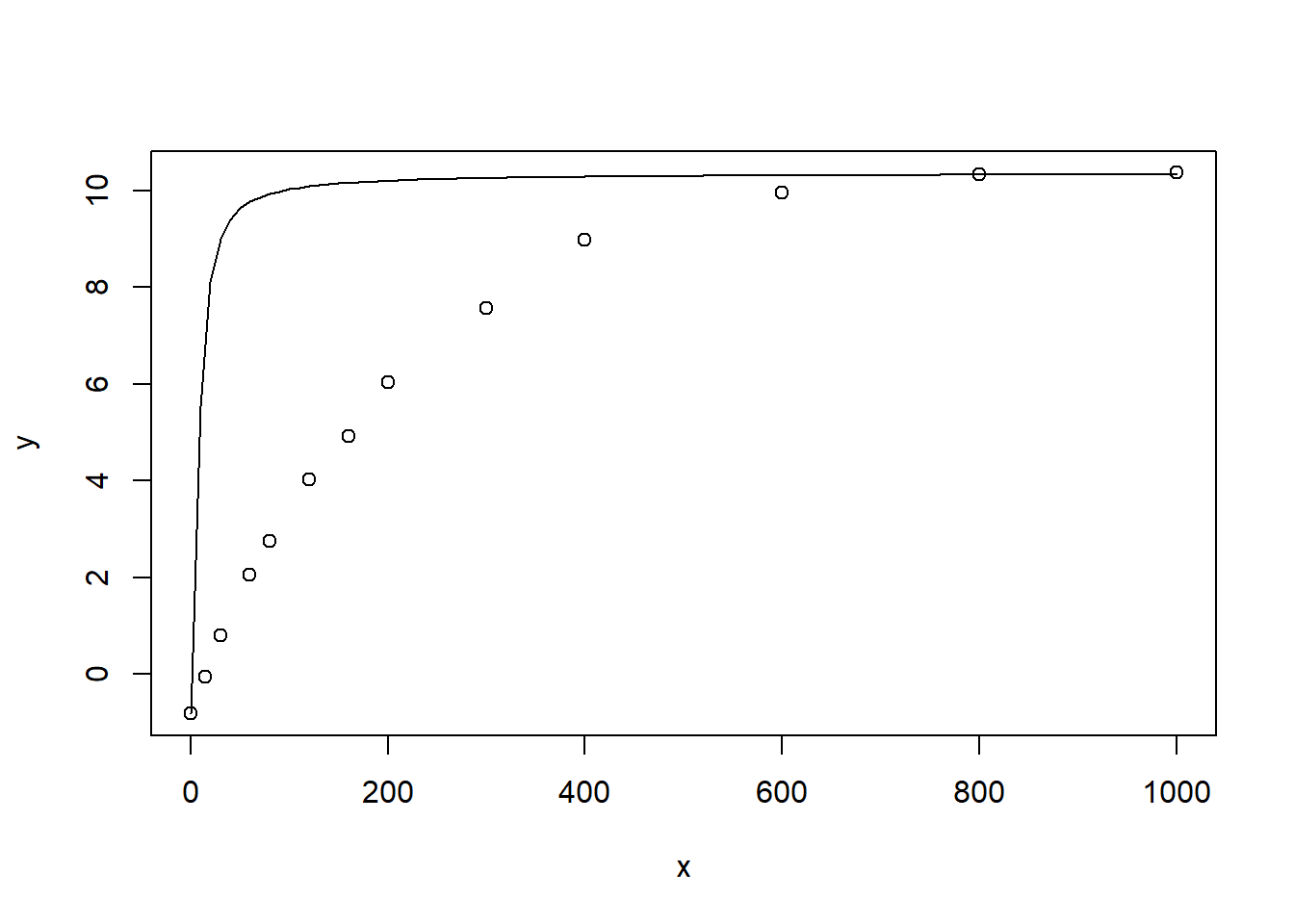
图 9.1: 初步判断 alpha 的初始值

观察上图 9.1 的结果可以看到，曲线在 0-600 的范围内，拟合值明显偏大，观察模型的方程式，以及其他起始值的设定方式，我们初步判断 alpha 的值偏大，于是乎我们将其改小观察，观察曲线和测量点的重合仍然不是很好，我们尝试修改 theta 值与 alpha 值（也即曲线高于测量点，则需要减小纵坐标的值，低于测量点，则需要增加该值，该过程省略，我大概设置了五分钟完成），最终得出的结果如下：

plot(y ~ x, data = test)
curve(expfct(x, Am = (max(lrc_A)-min(lrc_A)),
     alpha=0.06, Rd=-min(lrc_A), theta=0.82), add = TRUE)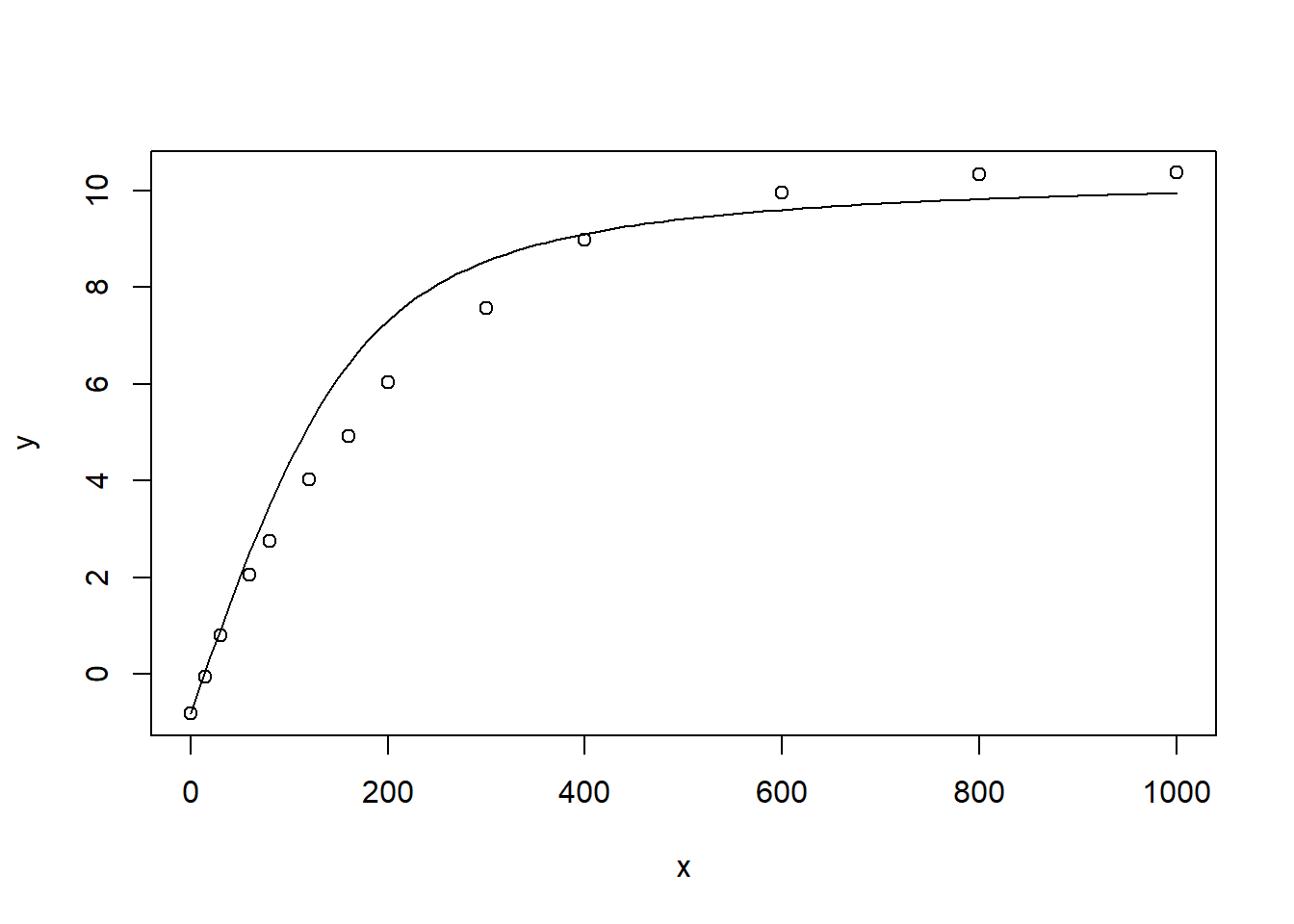

图 9.2: 初修正后断 alpha 的初始值

图 9.2 尽管看上去效果仍然不满意，但我们可试着进行拟合，看能否得到显著差异的结果：

lrcnls_manual <- nls(lrc_A ~ 
        (1/(2*theta))*
        (alpha*lrc_Q+Am-sqrt((alpha*lrc_Q+Am)^2 - 
                               4*alpha*theta*Am*lrc_Q))- 
        Rd, start=list(Am=(max(lrc_A)-min(lrc_A)),
                       alpha=0.03,Rd=-min(lrc_A),theta=0.6))
summary(lrcnls_manual)

## 
## Formula: lrc_A ~ (1/(2 * theta)) * (alpha * lrc_Q + Am - sqrt((alpha * 
##     lrc_Q + Am)^2 - 4 * alpha * theta * Am * lrc_Q)) - Rd
## 
## Parameters:
##        Estimate Std. Error t value Pr(>|t|)    
## Am    12.307585   0.406741  30.259 2.30e-10 ***
## alpha  0.045706   0.003423  13.352 3.09e-07 ***
## Rd     0.656642   0.132646   4.950 0.000791 ***
## theta  0.707518   0.079739   8.873 9.59e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1852 on 9 degrees of freedom
## 
## Number of iterations to convergence: 7 
## Achieved convergence tolerance: 4.601e-06

# 对拟合之后的结果作图，观察使用我们的估计值，
# 迭代的最终值与元数据的重合程度
plot(y ~ x, data = test, ylim = c(-2, 14))
curve(expfct(x, Am = 12.307586,
     alpha=0.045706, Rd= 0.656643, theta=0.707518), add = TRUE)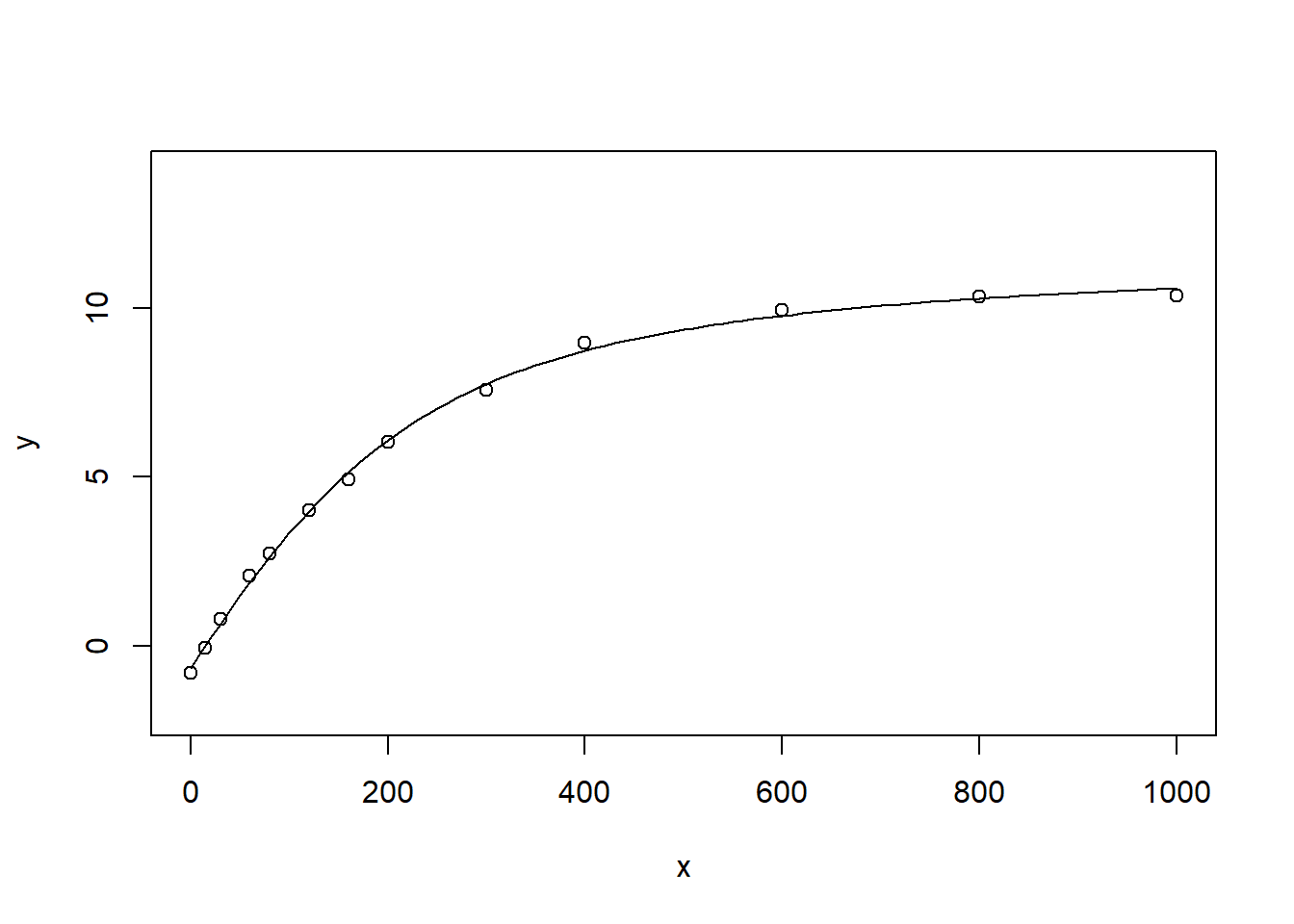

图 9.3: 检验作图法的初始值判断

从 9.3 的呈现以及 F 检验的 p 值来讲，图形已经比较完美了。也就是说尽管我们作图的时候看到重合度并不高，但是非线性拟合本来就是一个迭代的过程，只要我们的数据与真实值相差不大，还是能够得到完美结果的。

9.2.2 直观展示

上面的表述太啰嗦，直接用下面的图形说明一下，其中 alhpa 的取值在此处选择从 0.01 到 0.07，每次增加 0.05，其他值分别为 Am = 12.31, Rd= 0.66, theta=0.71 （此处为展示效果和方便，将这些值直接按照拟合结果设定了，实际差别不大）

library(ggplot2)
library(purrr)

lrc <- read.csv("data/nlstest.csv")

# 光响应曲线比较简单，我们将需要的数据直接提取，方便后面操作
lrc_Q <- lrc$Qin
lrc_A <- lrc$A
n <- length(lrc_A)


alp <- paste0("a=", seq(0.01, 0.07, by = 0.005))
alpn <- rep(alp, each = n)

expfct <- function(x, Am, alpha, Rd, theta) {(1/(2 * theta)) * (alpha * x + Am - sqrt((alpha * x + Am)^2 - 4 * alpha * theta * Am * x)) - Rd
}

paras <- data.frame(alpha = rep(seq(0.01, 0.07, by = 0.005), each = n), 
           x = rep(lrc_Q, n), Am = rep(12.31, n), Rd = rep(0.66, n), 
           theta = rep(0.71, n))
y = unlist(pmap(paras, expfct))

show <- data.frame(x = rep(lrc_Q, 14),
           y = c(lrc_A, y), 
           a = factor(c(rep("measured", n), alpn),
           level = c("measured", alp)
             ))

ggplot(data = show, aes(x, y, group = a, color=a)) + 
  geom_point() + 
  geom_smooth(se = FALSE)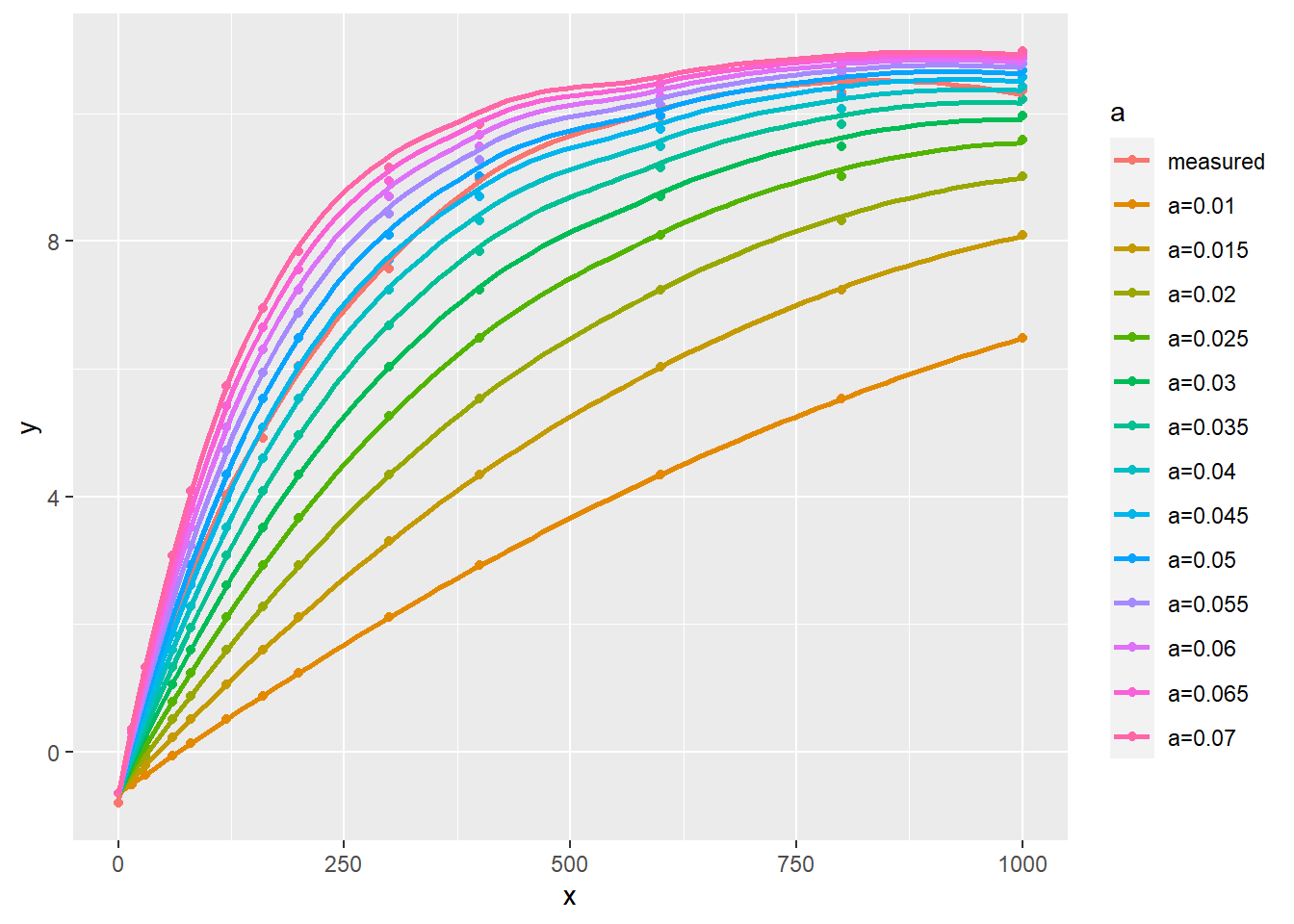

图 9.4: 多个 alpha 取值的差异

从上图 9.4 我们我们可以看到，实测值在 alpha =0.04 和 alpha = 0.05 两条曲线之间，在 0.045 时最接近测量点，也就是我们把初始值设为 0.04 和 0.05 之间最接近，本例中可认为是0.045，实际这三个值均可。

9.3 自动多次尝试法

该方法实际为使用 nls2 来实现，具体方法参考 Bouvier and Huet (1994) 的文章，可简单概括为使用一系列的起始值梯度（例如下面的代码中， alpha 的取值在 0.01 到 0.08 之间），然后软件循序使用不同的起始值，即排列组合所有的起始值序列，最终找到合适的值，具体实现如下：

library(nls2)

grid.test <- expand.grid(list(
  Am=c(12),
  alpha = seq(0.01, 0.08, by =0.01),
  Rd = seq(0, 3),
  theta=seq(0.1, 1, by = 0.1)
  ))

lrcnls2 <- nls2(lrc_A ~ 
        (1/(2*theta))*
        (alpha*lrc_Q+Am-sqrt((alpha*lrc_Q+Am)^2 - 
                               4*alpha*theta*Am*lrc_Q))- 
        Rd, start = grid.test, algorithm = "brute-force")

## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model
## Error in numericDeriv(form[[3L]], names(ind), env, central = nDcentral) : 
##   Missing value or an infinity produced when evaluating the model

summary(lrcnls2)

## 
## Formula: lrc_A ~ (1/(2 * theta)) * (alpha * lrc_Q + Am - sqrt((alpha * 
##     lrc_Q + Am)^2 - 4 * alpha * theta * Am * lrc_Q)) - Rd
## 
## Parameters:
##        Estimate Std. Error t value Pr(>|t|)    
## Am    12.000000   0.623023  19.261 1.27e-08 ***
## alpha  0.050000   0.006414   7.795 2.72e-05 ***
## Rd     1.000000   0.260153   3.844  0.00394 ** 
## theta  0.800000   0.102143   7.832 2.62e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3663 on 9 degrees of freedom
## 
## Number of iterations to convergence: 320 
## Achieved convergence tolerance: NA

通过结果可以看到，虽然和之前采用手动方法判定的结果比较接近，但是还是略有差异，可以看一下他们各自的结果同测量值的重合程度：

plot(lrc_Q, lrc_A)
lines(lrc_Q,  predict(lrcnls2), col="red")
lines(lrc_Q,  predict(lrcnls_manual), col="blue")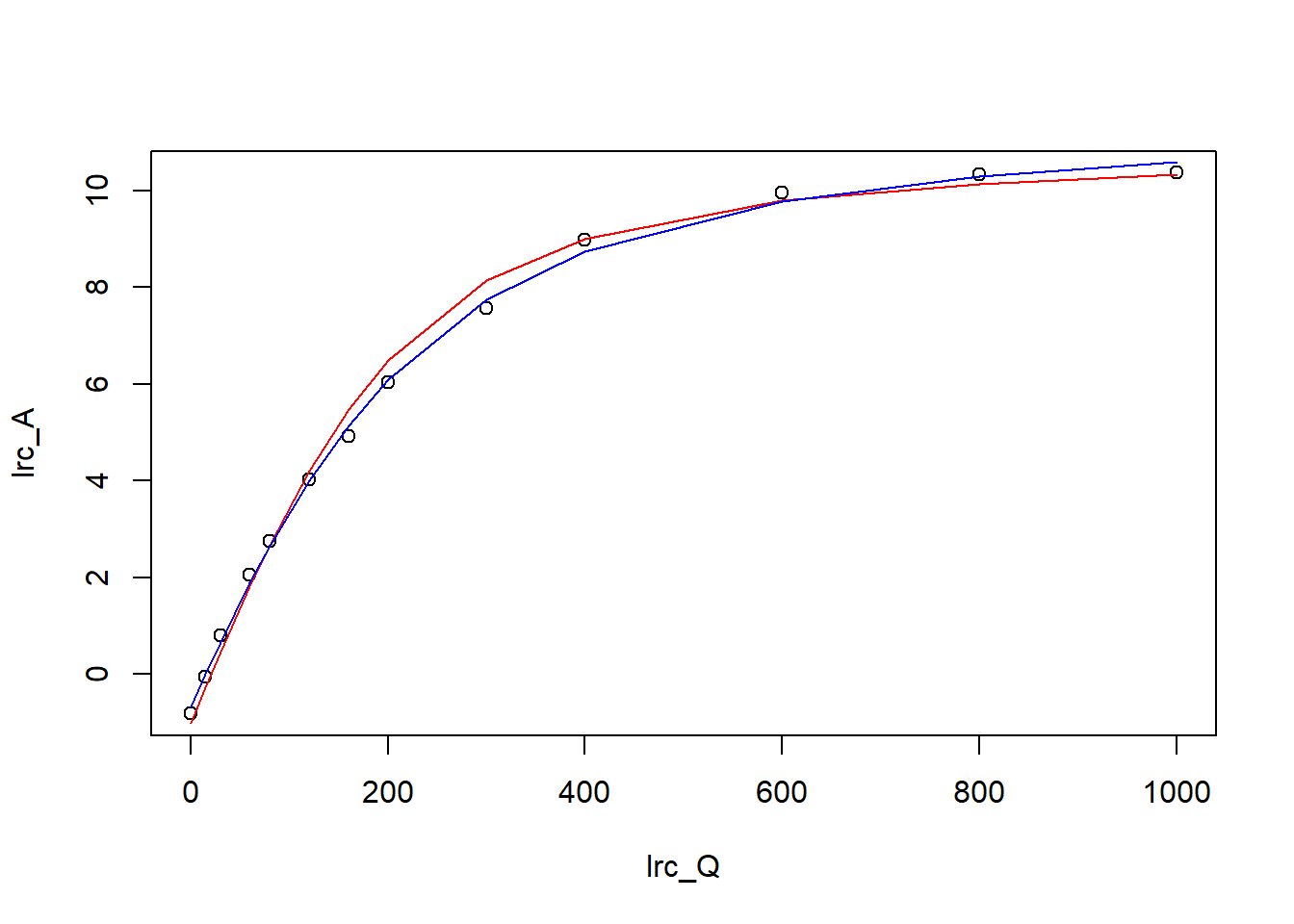

图 9.5: 两种方法结果的对比展示

图 9.5 可以看到，使用 nls2 的拟合结果似乎和测量值更匹配，当然这只是第一印象，后续的判断还要进一步通过 F 检验、 AIC、BIC 等统计方式才能判定。

9.4 小结

采用如上三种方式都可以有效的解决起始值的问题，nlsLM 操作上更易实现，对初始值的大小不敏感，但设置不能太离谱，否则仍然会报错。作图比对法操作上更麻烦一些，但是这种方式一定能得出合理的初始值设置。采用 nls2 类似于将手动作图方式自动化，类似于 SPSS 中非线性拟合中需要给出一个初始值的范围，且该范围不能过大。如有一定的经验，操作起来将非常迅速。

需要注意的是，这三种方法结合起来使用会更好，例如，即使使用 nlsLM 的结果不合理，也可以参考他们参数的范围（部分结果也可能是差异显著），然后将这些结果用于手动作图判定参数或者 nls2 中判定参数范围，或者使用作图法确定大致的范围，将该范围输入到 nls2 中，这样会节省时间，也更加方便。

参考文献

Bouvier, Annie, and Sylvie Huet. 1994. “Nls2 Nonlinear Regression by s PLUS Functions.” Computational Statistics & Data Analysis 18 (1): 187–90.

Elzhov, Timur V., Katharine M. Mullen, Andrej Nikolai Spiess, and Ben Bolker. 2016. “Minpack.lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds.”

第 9 章 关于非线性拟合的初始值