第 6 章 光合气孔导度耦合模型
Remko A. Duursma (2015) 对于气体交换耦合模型的简述如下 11:
- 对于 FvCB 模型有:
\[\begin{equation} A_n = min(A_c, A_j)-R_d \tag{6.1} \end{equation}\]
- 在假定 gm 为恒定的前提下:
\[\begin{equation} C_c = C_i - \frac{A_n}{g_m} \tag{6.2} \end{equation}\]
- 根据 Ficker 定理
\[\begin{equation} A_n = \frac{g_s}{1.6}(C_a - C_i) \tag{6.3} \end{equation}\]
以及前文 4.1 提到的气孔导度模型
\[\begin{equation} g_s = g_0 + g_1 \frac{A_n}{C_a} f(D) \tag{6.4} \end{equation}\]
整合公式 (6.1), (6.2), (6.3) 和 (6.4),气体交换耦合模型有很多更大尺度上的应用,例如 R. A. Duursma and Medlyn (2012) 和 wang1998a,可用于预测 An,gs 和蒸腾速率对主要环境驱动因子的响应(除土壤水分),并包含了主要的叶片性状(g1,Vcmax, Jmax, Rd 以及他们的温度依赖性)。
6.1 Photosyn 函数
Photosyn 为耦合的光合–气孔导度模型,基于 Farquhar 光合模型和 Ball-Berry 气孔导度模型。
Photosyn(VPD = 1.5, Ca = 400, PPFD = 1500,
Tleaf = 25, Patm = 100,RH = NULL,
gsmodel = c("BBOpti", "BBLeuning",
"BallBerry", "BBdefine"),
g1 = 4, g0 = 0, gk = 0.5, vpdmin = 0.5,
D0 = 5, GS = NULL, BBmult = NULL,
alpha = 0.24, theta = 0.85, Jmax = 100,
Vcmax = 50, gmeso = NULL, TPU = 1000,
alphag = 0, Rd0 = 0.92, Q10 = 1.92,
Rd = NULL, TrefR = 25, Rdayfrac = 1,
EaV = 82620.87, EdVC = 0, delsC = 645.1013,
EaJ = 39676.89, EdVJ = 2e+05, delsJ = 641.3615,
GammaStar = NULL, Km = NULL, Ci = NULL,
Tcorrect = TRUE,returnParsOnly = FALSE,
whichA = c("Ah", "Amin", "Ac", "Aj"))
Aci(Ci, ...)因为是光合气孔导度模型的耦合,故而参数与之前的函数相同,参见 3.5.2 和 4.4 部分的内容。
6.1.1 Photosyn 使用举例
library(plantecophys)
# 仅使用下面几个参数运行模型
#(其他参数使用默认值)
# 利用已测量或计算的参数
Photosyn(VPD=2, g1=4, Ca=500)## Ci ALEAF GS ELEAF Ac Aj Ap Rd VPD Tleaf
## 1 369.3981 14.19466 0.1706377 3.412753 15.12654 17.03685 1000 0.92 2 25
## Ca Cc PPFD Patm
## 1 500 369.3981 1500 100# 部分参数相同,而某一参数或某几个参数不同时,
# 可以将不同的参数设置为一个序列(vectors)
r <- Photosyn(VPD=seq(0.5, 4, length=25),
Vcmax=50, Jmax=100)
with(r, plot(VPD, ALEAF, type='l'))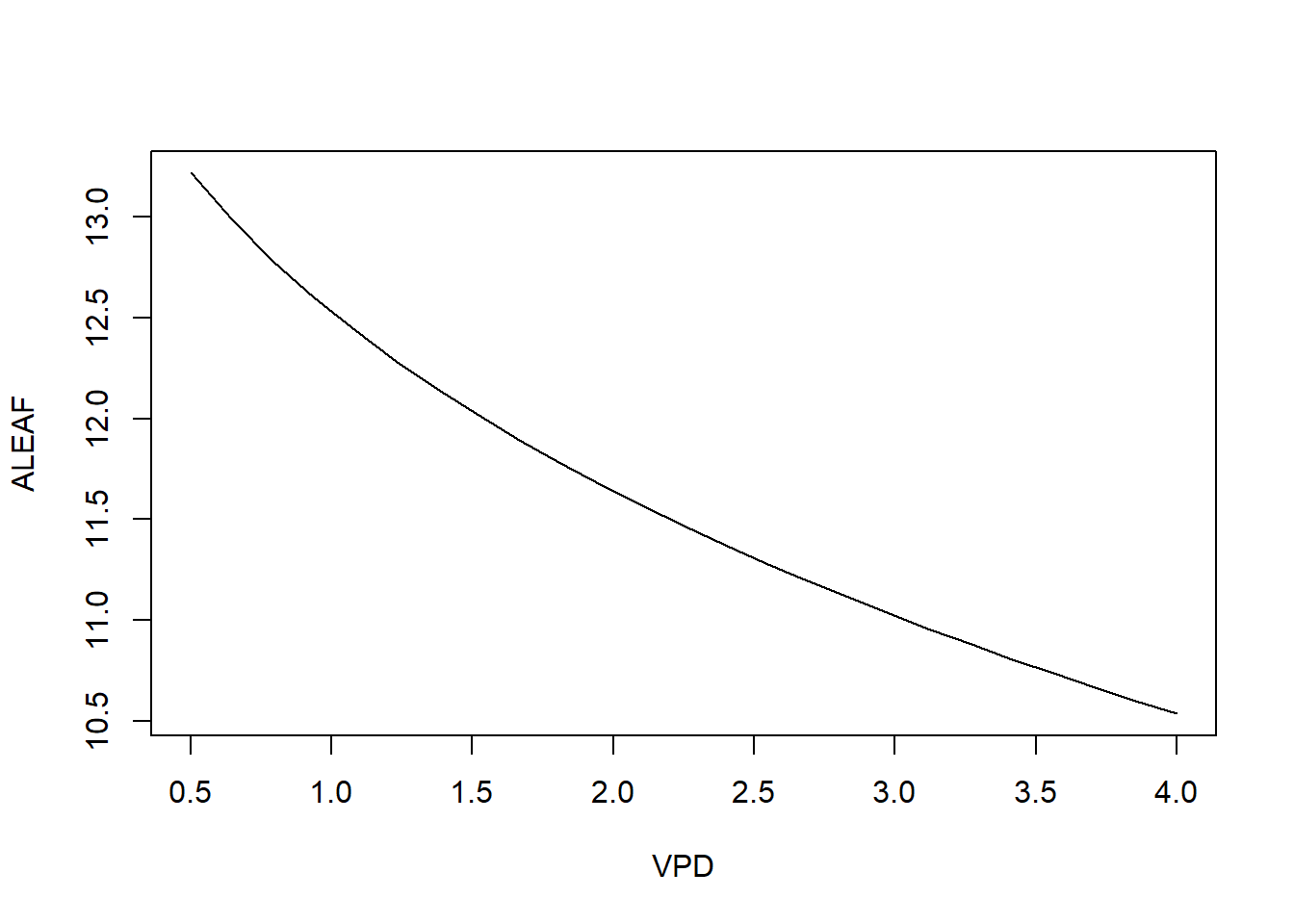
图 6.1: VPD VS. An
不同 VPD 下的光合速率见 6.1。
# 设定叶肉导度的拟合
run1 <- Photosyn(PPFD=seq(50,1000,length=25),
gmeso=0.15, Vcmax=40, Jmax=85)
with(run1, plot(PPFD, GS, type='l'))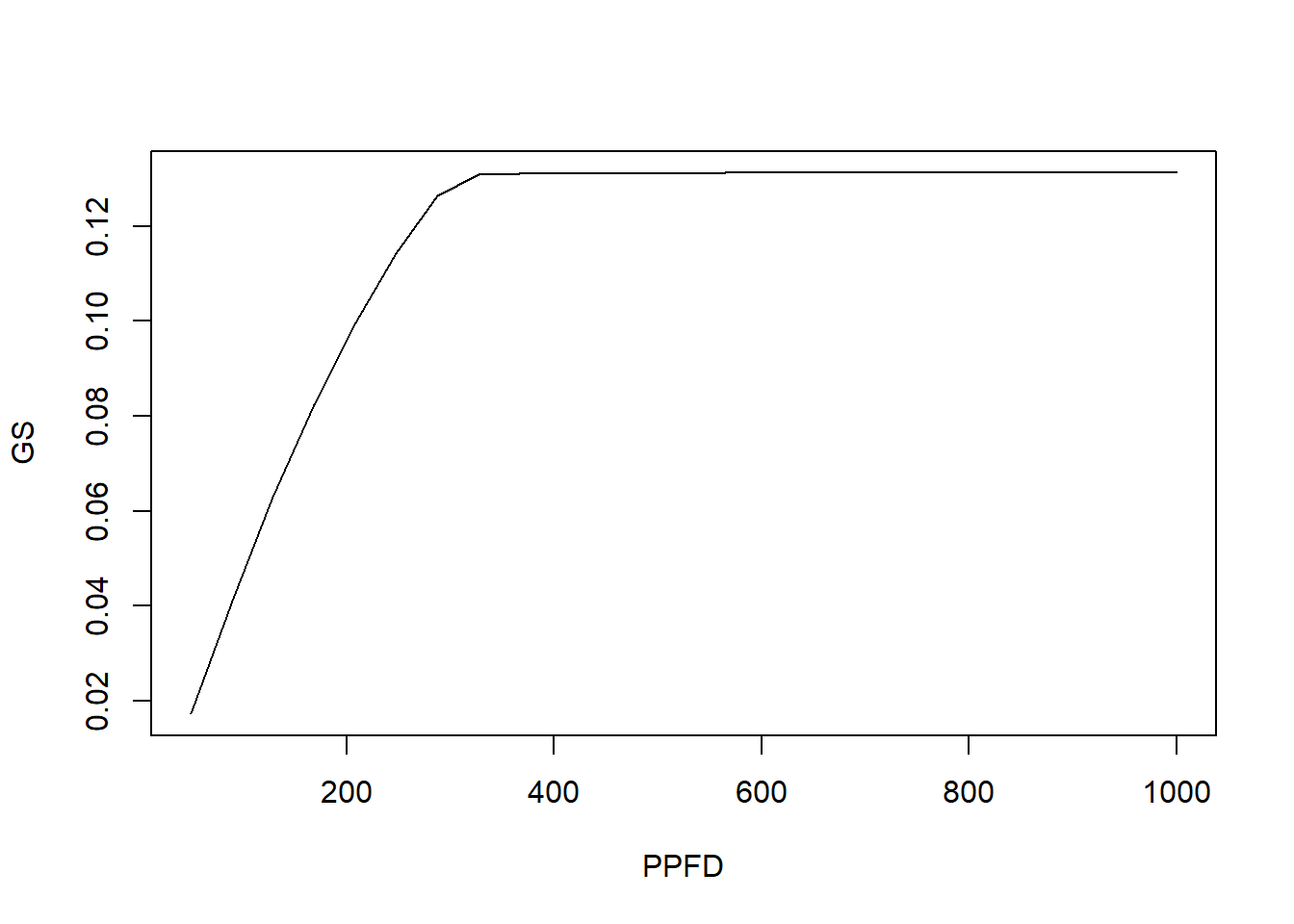
图 6.2: PPFD VS. GS
# 运行ACi曲线数据(提供Ci值而不是计算)
arun1 <- Aci(Ci=seq(50, 1200, length=101),
Vcmax=40, Jmax=85)
arun2 <- Aci(Ci=seq(50, 1200, length=101),
Vcmax=30, Jmax=70)
with(arun1, plot(Ci, ALEAF, type='l'))
with(arun2, points(Ci, ALEAF, type='l', lty=5))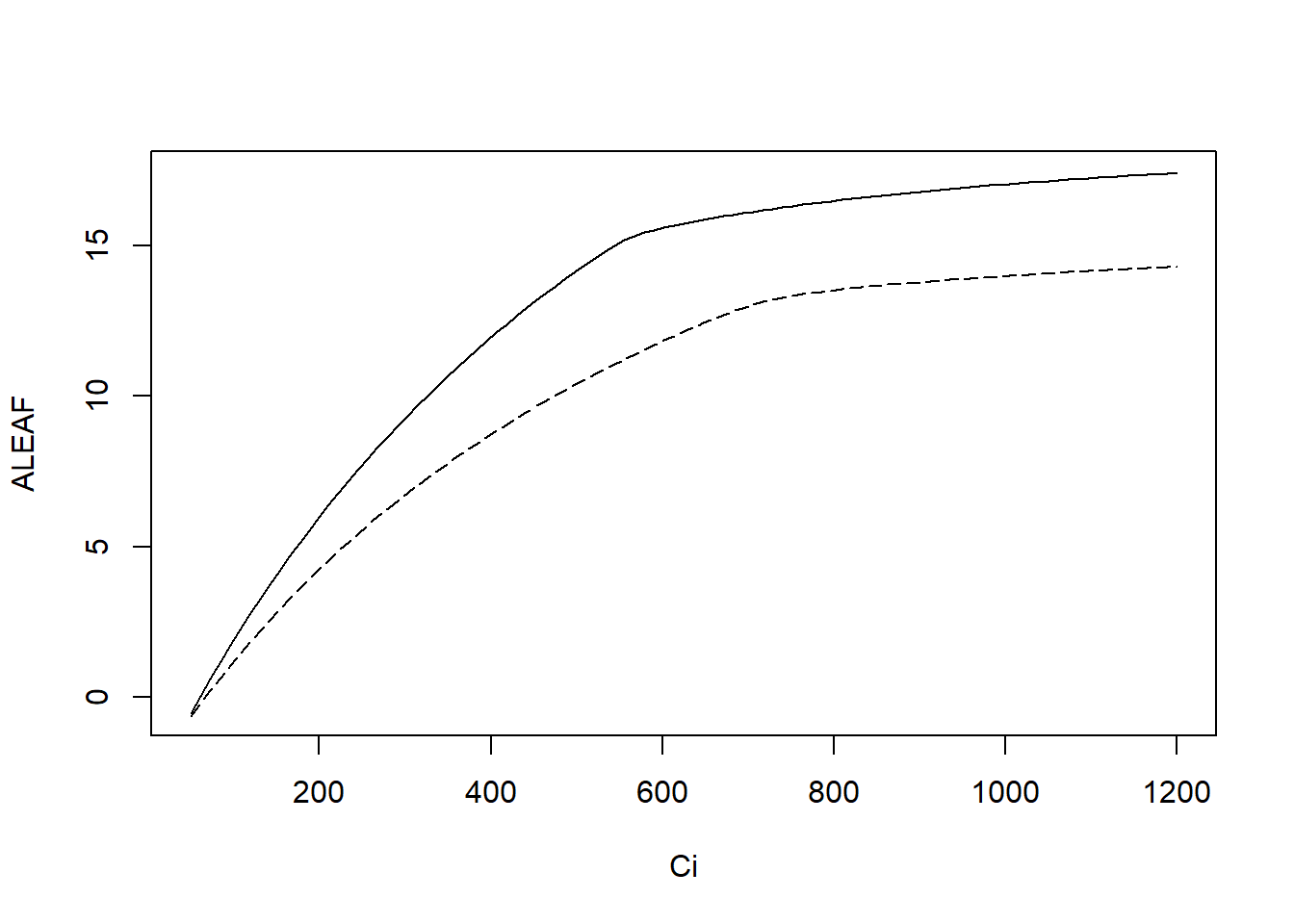
图 6.3: PPFD VS. GS
不同 ci 下的光合速率见 ??。
# 找出CO2需求和供给的交叉点
# 设定部分参数
gs <- 0.2 # 对水的气孔导度
Ca <- 400 # 外部CO2
gctogw <- 1.57 # 转换系数
gc <- gs / gctogw # 对 CO2 的气孔导度
# 需求曲线
p <- Aci(seq(60,500,length=101), Ca=400)
# 提供气孔导度及交叉点
g <- Photosyn(GS=gs, Ca=Ca)
# 交叉点可视化
par(yaxs="i")
with(p, plot(Ci, ALEAF, type='l',
ylim=c(0,max(ALEAF))))
with(g, points(Ci, ALEAF, pch=19, col="red"))
abline(gc * Ca, -gc, lty=5)
legend("topleft", c(expression(
"Demand:"~~A==f(C[i])),
expression("Supply:"~~A==g[c]*(C[a]-C[i])),
"Operating point"),
lty=c(1,5,-1),pch=c(-1,-1,19),
col=c("black","black","red"),
bty='n', cex=0.9)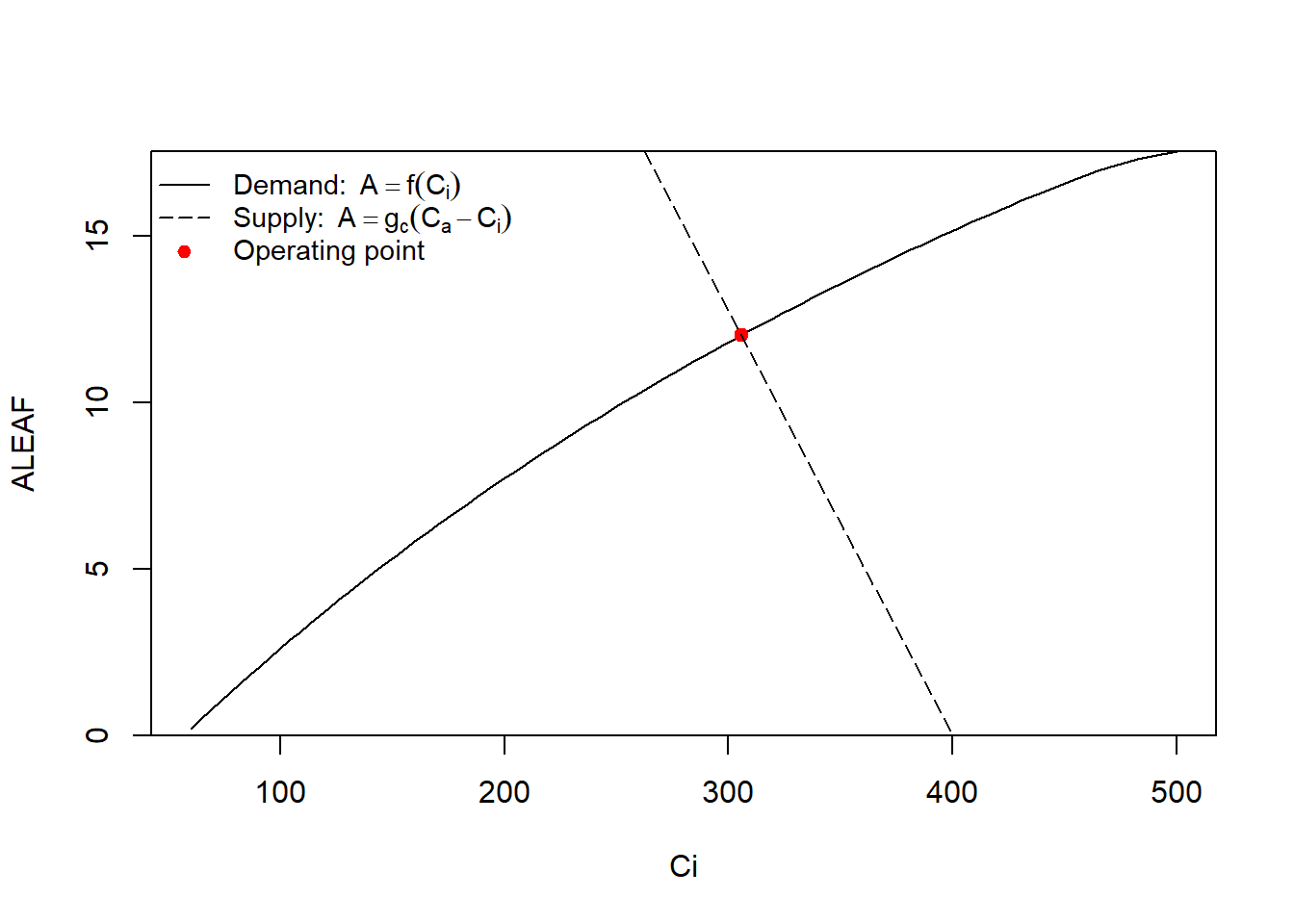
图 6.4: supply VS. demand
需求与供给的作图 6.4。
6.2 PhotosynEB 函数
使用同 Photosyn,只不过使用能量平衡法来计算叶温。
目前版本尚存在bug,不能直接提供 GS 来计算,否则会出现未知错误。
6.3 PhotosynTuzet 函数
同样为光合气孔导度耦合模型,只不过基于 Tuzet, Perrier, and Leuning (2003) 的气孔导度模型,现将其描述如下:
\[\begin{equation} g_{co2} = g_0 + \frac{a A}{C_i - \Gamma} f_{\Psi v} \tag{6.5} \end{equation}\]
其中 gco2 为对 CO2 的气孔导度, g0 是残余导度(residual conductance)(在补偿点时限制 gCO2 的值), A 为光合速率,Ci 为胞间二氧化碳浓度,\(\Gamma\) 为 CO2 补偿点,a 是经验系数。
一个根据经验的逻辑方程用于描述气孔对水势的敏感性:
\[\begin{equation} f_{\Psi v} = \frac{1 + exp(s_f \Psi_f)}{1 + exp(s_f(\Psi_f - \Psi_v))} \tag{6.6} \end{equation}\]
\(\Psi_v\) 是指叶片水势,\(\Psi_f\) 是参比势能, 该方程假设在水势接近于 0 时,气孔对叶片水势不敏感,并且气孔随着 \(\Psi_v\) 的下降快速关闭。\(\Psi_f\) 和 \(s_f\) (曲线形状参数) 依赖于不同物种的形态学适应以及生长过程中所处的环境。
6.3.1 PhotosynTuzet 的参数
除 Tuzet, Perrier, and Leuning (2003) 模型中使用的参数外,其他参数都继承了 Photosyn 的参数
PhotosynTuzet(g1 = 8, Ca = 400, psis = 0,
kl = 2, sf = 3, psif = -2,
...)- g1:斜率参数,要远比
fitBB中的大。 - Ca:外界大气 CO2 浓度
- psis,土壤水势(Mpa)。
- kl:Leaf-specific hydraulic conductance(叶片导水参数 (\(mmol \cdot m^{-2} \cdot s^{-1} \cdot MPa^{-1}\)),叶片蒸腾量、叶片面积及叶片水势计算)。
- sf:曲线形状参数。
- 在气孔导度为最大值 50% 时的叶片水势。